
【题目】已知函数f(x)=2x3+bx2+cx,其导函数y=f′(x)的图象(如图所示)经过点(1,0),(2,0). (Ⅰ)求f(x)的解析式;
(Ⅱ)若方程f(x)﹣m=0恰有2个根,求m的值.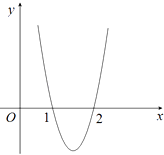
【答案】解:(Ⅰ)依题意,可得f'(x)=6x2+2bx+c=0的解为x=1,x=2, 故 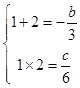 解得
解得 ![]()
所以f(x)=2x3﹣9x2+12x.
(Ⅱ)f'(x)=6x2﹣18x+12=6(x﹣1)(x﹣2),
当f'(x)>0时,x<1或x>2;
当f'(x)<0时,1<x<2.
所以函数f(x)的单调增区间为(﹣∞,1)和(2,+∞),单调减区间为(1,2),
当x=1时,f(x)极大=5,当x=2时,f(x)极小=4.
故方程f(x)﹣m=0恰有2个根,得m=4或m=5
【解析】(Ⅰ)根据图象可得得f'(x)=6x2+2bx+c=0的解为x=1,x=2,根据根与系数的关系,联立方程组求解即可;(Ⅱ)根据导数求出函数的单调区间,求出相应函数值,即可求实数m的值.
【考点精析】利用基本求导法则和利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.71828…为自然对数的底数.
(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=a,an+1= ![]() (n∈N*).
(n∈N*).
(1)求a2 , a3 , a4;
(2)猜测数列{an}的通项公式,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域是D,若存在常数m、M,使得m≤f(x)≤M对任意x∈D成立,则称函数f(x)是D上的有界函数,其中m称为函数f(x)的下界,M称为函数f(x)的上界;特别地,若“=”成立,则m称为函数f(x)的下确界,M称为函数f(x)的上确界. (Ⅰ)判断 ![]() 是否是有界函数?说明理由;
是否是有界函数?说明理由;
(Ⅱ)若函数f(x)=1+a2x+4x(x∈(﹣∞,0))是以﹣3为下界、3为上界的有界函数,求实数a的取值范围;
(Ⅲ)若函数 ![]() ,T(a)是f(x)的上确界,求T(a)的取值范围.
,T(a)是f(x)的上确界,求T(a)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinx﹣bcosx(a,b为常数,a≠0,x∈R)在x= ![]() 处取得最大值,则函数y=f(x+
处取得最大值,则函数y=f(x+ ![]() )是( )
)是( )
A.奇函数且它的图象关于点(π,0)对称
B.偶函数且它的图象关于点( ![]() ,0)对称
,0)对称
C.奇函数且它的图象关于点( ![]() ,0)对称
,0)对称
D.偶函数且它的图象关于点(π,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的单调函数f(x)满足:f(x+y)=f(x)+f(y),若F(x)=f(asinx)+f(sinx+cos2x﹣3)在(0,π)上有零点,则a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() cos(2x﹣
cos(2x﹣ ![]() ).
).
(1)若sinθ=﹣ ![]() ,θ∈(
,θ∈( ![]() ,2π),求f(θ+
,2π),求f(θ+ ![]() )的值;
)的值;
(2)若x∈[ ![]() ,
, ![]() ],求函数f(x)的单调减区间.
],求函数f(x)的单调减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com