
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,求出最大的整数
的图象的下方?若存在,求出最大的整数![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(参考数据: ![]() )
)
【答案】(1)所求切线的方程为![]() (2)存在实数
(2)存在实数![]() 满足题意,且最大整数
满足题意,且最大整数![]() 的值为
的值为![]() .
.
【解析】【试题分析】(1)依据题设先求出切点坐标,再对函数求导,进而求出在切点处的导函数值即为切线的斜率,然后运用点斜式求出切线方程;(2)先依据题设建立不等式![]() ,进而将问题转化为即
,进而将问题转化为即![]() 对
对![]() 恒成立。然后构造函数
恒成立。然后构造函数![]() ,再求导数
,再求导数![]() , 令
, 令![]() ,则
,则![]() ,
,
因为![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
, ![]() ,
,
且![]() 的图象在
的图象在![]() 上连续,所以存在
上连续,所以存在![]() ,使得
,使得![]() ,即
,即![]() ,最后判定当
,最后判定当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增,
单调递增,
则![]() 取到最小值
取到最小值![]()
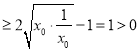 ,
,
所以![]() ,即
,即![]() 在区间
在区间![]() 内单调递增. 所以
内单调递增. 所以![]() ,即存在实数
,即存在实数![]() 满足题意,且最大整数
满足题意,且最大整数![]() 的值为
的值为![]() 。
。
解:(1)因为![]() ,所以
,所以![]() ,则所求切线的斜率为
,则所求切线的斜率为![]() .
.
又![]() ,故所求切线的方程为
,故所求切线的方程为![]() .
.
(2)假设存在实数![]() 满足题意,则不等式
满足题意,则不等式![]() 对
对![]() 恒成立.
恒成立.
即![]() 对
对![]() 恒成立
恒成立
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
, ![]() ,/span>
,/span>
且![]() 的图象在
的图象在![]() 上连续,所以存在
上连续,所以存在![]() ,使得
,使得![]() ,即
,即![]() ,
,
则![]() ,
,
所以当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增,
单调递增,
则![]() 取到最小值
取到最小值![]()
 ,
,
所以![]() ,即
,即![]() 在区间
在区间![]() 内单调递增.
内单调递增.
所以![]() ,
,
所以存在实数![]() 满足题意,且最大整数
满足题意,且最大整数![]() 的值为
的值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为:
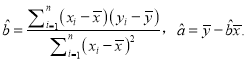
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由甲、乙两位男生和丙、丁两位女生组成的四人冲关小组,参加由安徽卫视推出的大型户外竞技类活动《男生女生向前冲》.活动共有四关,若四关都闯过,则闯关成功,否则落水失败.设男生闯过一至四关的概率依次是![]() ,女生闯过一至四关的概率依次是
,女生闯过一至四关的概率依次是![]() .
.
(Ⅰ)求男生甲闯关失败的概率;
(Ⅱ)设![]() 表示四人冲关小组闯关成功的人数,求随机变量
表示四人冲关小组闯关成功的人数,求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】班主任为了对本班学生的考试成绩进行分析,决定从本班24名女同学,18名男同学中随机抽取一个容量为7的样本进行分析.
(1)如果按照性别比例分层抽样,可得到多少个不同的样本?(写出算式即可,不必计算出结果)
(2)如果随机抽取的7名同学的数学,物理成绩(单位:分)对应如下表:
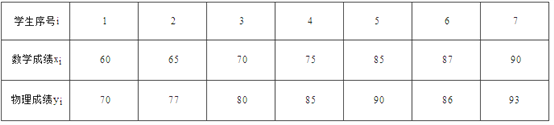
若规定85分以上(包括85分)为优秀,从这7名同学中抽取3名同学,记3名同学中数学和物理成绩均为优秀的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有5名男司机,4名女司机,需选派5人运货到吴忠.
(1)如果派3名男司机、2名女司机,共有多少种不同的选派方法?
(2)至少有两名男司机,共有多少种不同的选派方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,并且内切于定圆
,并且内切于定圆![]() .
.
(1)求动圆圆心![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 上存在两个点
上存在两个点![]() ,(1)中曲线上有两个点
,(1)中曲线上有两个点![]() ,并且
,并且![]() 三点共线,
三点共线, ![]() 三点共线,
三点共线, ![]() ,求四边形
,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的图象是由y=sin2x向右平移 ![]() 得到,则下列结论正确的是( )
得到,则下列结论正确的是( )
A.f(0)<f(2)<f(4)
B.f(2)<f(0)<f(4)
C.f(0)<f(4)<f(2)
D.f(4)<f(2)<f(0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com