
【题目】为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查,得到了如下的统计结果:

(1)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数;
(2)完成联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”.

附:![]() ,其中n=a+b+c+d为样本容量.
,其中n=a+b+c+d为样本容量.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
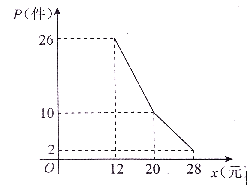
(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),曲线C2的参数方程为
为参数),曲线C2的参数方程为![]() (
(![]() 为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α 与C1,C2 各有一个交点.当 α=0时,这两个交点间的距离为2,当 α=
为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α 与C1,C2 各有一个交点.当 α=0时,这两个交点间的距离为2,当 α=![]() 时,这两个交点重合.
时,这两个交点重合.
(1) 求曲线C1,C2的直角坐标方程
(2) 设当 α=![]() 时,l与C1,C2的交点分别为A1,B1,当 α=-
时,l与C1,C2的交点分别为A1,B1,当 α=-![]() 时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1) 试说明函数![]() 的图象是由函数
的图象是由函数![]() 的图象经过怎样的变换得到的;
的图象经过怎样的变换得到的;
(2)若函数![]() ,试判断函数
,试判断函数![]() 的奇偶性,并用反证法证明函数
的奇偶性,并用反证法证明函数![]() 的最小正周期是
的最小正周期是![]() ;
;
(3)求函数![]() 的单调区间和值域.
的单调区间和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在本市某旧小区改造工程中,需要在地下铺设天燃气管道.已知小区某处三幢房屋分别位于扇形![]() 的三个顶点上,点
的三个顶点上,点![]() 是弧
是弧![]() 的中点,现欲在线段
的中点,现欲在线段![]() 上找一处开挖工作坑
上找一处开挖工作坑![]() (不与点
(不与点![]() ,
,![]() 重合),为铺设三条地下天燃气管线
重合),为铺设三条地下天燃气管线![]() ,
,![]() ,
,![]() ,已知
,已知![]() 米,
米,![]() ,记
,记![]() ,该三条地下天燃气管线的总长度为
,该三条地下天燃气管线的总长度为![]() 米.
米.

(1)将![]() 表示成
表示成![]() 的函数,并写出
的函数,并写出![]() 的范围;
的范围;
(2)请确定工作坑![]() 的位置,使此处地下天燃气管线的总长度最小,并求出总长度的最小值.
的位置,使此处地下天燃气管线的总长度最小,并求出总长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是AC的中点,四边形BDEF是菱形,平面![]() 平面ABC,
平面ABC,![]() ,
,![]() ,
,![]() .
.
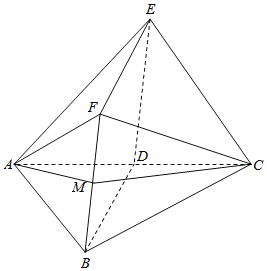
![]() 若点M是线段BF的中点,证明:
若点M是线段BF的中点,证明:![]() 平面AMC;
平面AMC;
![]() 求平面AEF与平面BCF所成的锐二面角的余弦值.
求平面AEF与平面BCF所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图(1)是某条公共汽车线路收支差额y关于乘客量x的图象.



(1)试说明图(1)上点A,点B以及射线AB上的点的实际意义;
(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的建议,如图(2)(3)所示,你能根据图象,说明这两种建议是什么吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com