
【题目】已知函数![]() .
.
(1)设![]() 是
是![]() 的极值点.求
的极值点.求![]() ,并求
,并求![]() 的单调区间;
的单调区间;
(2)证明:当![]() 时,
时,![]() .
.
【答案】(1) a=![]() ;f(x)在(0,2)单调递减,在(2,+∞)单调递增.
;f(x)在(0,2)单调递减,在(2,+∞)单调递增.
(2)证明见解析.
【解析】分析:(1)先确定函数的定义域,对函数求导,利用f ′(2)=0,求得a=![]() ,从而确定出函数的解析式,之后观察导函数的解析式,结合极值点的位置,从而得到函数的增区间和减区间;
,从而确定出函数的解析式,之后观察导函数的解析式,结合极值点的位置,从而得到函数的增区间和减区间;
(2)结合指数函数的值域,可以确定当a≥![]() 时,f(x)≥
时,f(x)≥![]() ,之后构造新函数g(x)=
,之后构造新函数g(x)=![]() ,利用导数研究函数的单调性,从而求得g(x)≥g(1)=0,利用不等式的传递性,证得结果.
,利用导数研究函数的单调性,从而求得g(x)≥g(1)=0,利用不等式的传递性,证得结果.
详解:(1)f(x)的定义域为![]() ,f ′(x)=aex–
,f ′(x)=aex–![]() .
.
由题设知,f ′(2)=0,所以a=![]() .
.
从而f(x)=![]() ,f ′(x)=
,f ′(x)=![]() .
.
当0<x<2时,f ′(x)<0;当x>2时,f ′(x)>0.
所以f(x)在(0,2)单调递减,在(2,+∞)单调递增.
(2)当a≥![]() 时,f(x)≥
时,f(x)≥![]() .
.
设g(x)=![]() ,则
,则![]()
当0<x<1时,g′(x)<0;当x>1时,g′(x)>0.所以x=1是g(x)的最小值点.
故当x>0时,g(x)≥g(1)=0.
因此,当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() ,对于任意实数k,下列直线被椭圆E截得的弦长与l:y=kx+1被椭圆E截得的弦长不可能相等的是( )
,对于任意实数k,下列直线被椭圆E截得的弦长与l:y=kx+1被椭圆E截得的弦长不可能相等的是( )
A. kx+y+k=0 B. kx-y-1=0
C. kx+y-k=0 D. kx+y-2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为![]() .不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
.不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
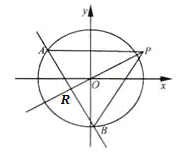
(Ⅰ)求椭圆C的方程;
(Ⅱ) 求![]() ABP的面积取最大时直线l的方程.
ABP的面积取最大时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过短轴的一个端点与两个焦点的圆的面积为
的焦距为2,过短轴的一个端点与两个焦点的圆的面积为![]() ,过椭圆
,过椭圆![]() 的右焦点作斜率为
的右焦点作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 垂直于
垂直于![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为侧棱
为侧棱![]() 上一点.
上一点.

(1)若![]() ,求证:
,求证:![]()
![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)在侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ? 若存在,求出线段
? 若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C:y=
中,曲线C:y=![]() 与直线
与直线![]() (
(![]() >0)交与M,N两点,
>0)交与M,N两点,
(Ⅰ)当k=0时,分别求C在点M和N处的切线方程;
(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过右焦点作垂直于椭圆长轴的直线交椭圆于
,过右焦点作垂直于椭圆长轴的直线交椭圆于![]() 两点,且
两点,且![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2) 设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若
两点,若![]() .
.
①求![]() 的值;
的值;
②求![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com