
ЁОЬтФПЁПдкКтбєЪаЁАДДШЋЙњЮФУїГЧЪаЁБЃЈМђГЦЁАДДЮФЁБЃЉЛюЖЏжаЃЌЪаНЬг§ОжЖдБОЪаAЃЌBЃЌCЃЌDЫФЫљИпжабЇаЃАДИїаЃШЫЪ§ЗжВуГщбљЃЌЫцЛњГщВщСЫ200ШЫЃЌНЋЕїВщЧщПіНјааећРэКѓжЦГЩЯТБэЃК
бЇаЃ | A | B | C | D |
ГщВщШЫЪ§ | 10 | 15 | 100 | 75 |
ЁАДДЮФЁБЛюЖЏжаВЮгыЕФШЫЪ§ | 9 | 10 | 80 | 49 |
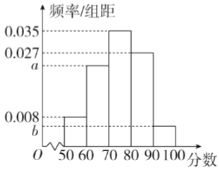
МйЩшУПУћИпжабЇЩњЪЧЗёВЮгыЁАДДЮФЁБЛюЖЏЪЧЯрЛЅЖРСЂЕФ
ЃЈ1ЃЉШєБОЪаЙВ8000УћИпжабЇЩњЃЌЙРМЦCбЇаЃВЮгыЁАДДЮФЁБЛюЖЏЕФШЫЪ§ЃЛ
ЃЈ2ЃЉдкЩЯБэжаДгAЃЌBСНаЃУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФЭЌбЇжаЫцЛњГщШЁ2ШЫЃЌЧѓЧЁКУAЃЌBСНаЃИїга1ШЫУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФИХТЪЃЛ
ЃЈ3ЃЉдкЫцЛњГщВщЕФ200УћИпжабЇЩњжаЃЌНјааЮФУїЫибјзлКЯЫижЪВтЦРЃЈТњЗжЮЊ100ЗжЃЉЃЌЕУЕНШчЩЯЕФЦЕТЪЗжВМжБЗНЭМЃЌЦфжа![]() ЃЎЧѓaЃЌbЕФжЕЃЌВЂЙРМЦВЮгыВтЦРЕФбЇЩњЕУЗжЕФжаЮЛЪ§ЃЎЃЈМЦЫуНсЙћБЃСєСНЮЛаЁЪ§ЃЉЃЎ
ЃЎЧѓaЃЌbЕФжЕЃЌВЂЙРМЦВЮгыВтЦРЕФбЇЩњЕУЗжЕФжаЮЛЪ§ЃЎЃЈМЦЫуНсЙћБЃСєСНЮЛаЁЪ§ЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉ3200ЃЈ2ЃЉ![]() ЃЈ3ЃЉжаЮЛЪ§ЮЊ
ЃЈ3ЃЉжаЮЛЪ§ЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓЕУCбЇаЃИпжаЩњЕФзмШЫЪ§ЃЌдйГЫвдCбЇаЃЫљеМЕФБШР§![]() ЃЌМШЕУД№АИЃЛ
ЃЌМШЕУД№АИЃЛ
ЃЈ2ЃЉЗжБ№БъМЧAЃЌBСНаЃУЛгаВЮгыЁАДДГЧЁБЛюЖЏЭЌбЇЃЌаДГіШЮШЁСНШЫЕФЫљгаЛљБОЪТМўЃЌбЁГіЦфжаТњзуЕФЬѕМўЕФЛљБОЪТМўЃЌгЩЙХЕфИХаЭЧѓИХТЪЕФЙЋЪНЃЌЧѓЕУД№АИЃЛ
ЃЈ3ЃЉгЩЦЕТЪЗжВМжБЗНЭМЕФУцЛ§ЮЊ1ЙЙНЈЗНГЬЃЌСЊЯЕвбжЊЧѓЕУ![]() ЃЌгЩЧАСНзщЕФЦЕТЪКЭаЁгк0.5ЃЌЧАШ§зщЕФЦЕТЪКЭДѓгк0.5ЃЌЫљвджаЮЛЪ§дкЕкШ§зщЃЌЧвдкЕкШ§зщжаЕФЦЕТЪЧЁеМ0.18ЃЌЧѓГіЕкШ§зщЕФГЄЖШМгЩЯ70ЃЌМШЕУД№АИ.
ЃЌгЩЧАСНзщЕФЦЕТЪКЭаЁгк0.5ЃЌЧАШ§зщЕФЦЕТЪКЭДѓгк0.5ЃЌЫљвджаЮЛЪ§дкЕкШ§зщЃЌЧвдкЕкШ§зщжаЕФЦЕТЪЧЁеМ0.18ЃЌЧѓГіЕкШ§зщЕФГЄЖШМгЩЯ70ЃЌМШЕУД№АИ.
ЃЈ1ЃЉCбЇаЃИпжаЩњЕФзмШЫЪ§ЮЊ![]() ЃЌ
ЃЌ
CбЇаЃВЮгыЁАДДЮФЁБЛюЖЏЕФШЫЪ§ЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉAаЃУЛгаВЮгыЁАДДГЧЁБЛюЖЏЕФет1ШЫМЧЮЊ![]() ЃЌBаЃУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФет5ШЫЗжБ№МЧЮЊ
ЃЌBаЃУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФет5ШЫЗжБ№МЧЮЊ![]()
![]()
![]()
![]()
![]() ЃЌ
ЃЌ
ШЮШЁ2ШЫЙВ15жжЧщПіЃЌШчЯТЃК![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ЃЌет15жжЧщПіЗЂЩњЕФПЩФмадЪЧЯрЕШЕФЃЎ
ЃЌет15жжЧщПіЗЂЩњЕФПЩФмадЪЧЯрЕШЕФЃЎ
ЩшЪТМўNЮЊГщШЁ2ШЫжаAЃЌBСНаЃИїга1ШЫУЛгаВЮгыЁАДДЮФЁБЛюЖЏЃЌга![]()
![]()
![]()
![]()
![]() ЃЌЙВ5жжЧщПіЃЎ
ЃЌЙВ5жжЧщПіЃЎ
дђ![]() ЃЎЙЪЧЁКУAЃЌBСНаЃИїга1ШЫУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФИХТЪЮЊ
ЃЎЙЪЧЁКУAЃЌBСНаЃИїга1ШЫУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФИХТЪЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉвРЬтвтЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЎ
ЃЎ
гж![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
вђЮЊ![]() ЃЌЫљвджаЮЛЪ§дкЕкШ§зщЃЌ
ЃЌЫљвджаЮЛЪ§дкЕкШ§зщЃЌ
ЫљвджаЮЛЪ§ЮЊ![]() ЃЎ
ЃЎ


 гЎдкПЮЬУУћЪІПЮЪБМЦЛЎЯЕСаД№АИ
гЎдкПЮЬУУћЪІПЮЪБМЦЛЎЯЕСаД№АИ ЬьЬьЯђЩЯПЮЪБЭЌВНбЕСЗЯЕСаД№АИ
ЬьЬьЯђЩЯПЮЪБЭЌВНбЕСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЙњЪЧЪРНчЕквЛВњСИДѓЙњЃЌЮвЙњСИЪГВњСПКмИпЃЌећЬхКмАВШЋАДее14вкШЫПкМЦЫуЃЌжаЙњШЫОљСИЪГВњСПдМЮЊ950НяЉБШШЋЧђШЫОљСИЪГВњСПИпСЫдМ250НяЃЎШчЭМЪЧжаЙњЙњМвЭГМЦОжЭјеОжа2010Љ2019ФъЃЌЮвЙњСИЪГВњСПЃЈЧЇЭђЖжЃЉгыФъФЉзмШЫПкЃЈЧЇЭђШЫЃЉЕФЬѕаЮЭМЃЌИљОнШчЭМПЩжЊдк2010Љ2019ФъжаЃЈ ЃЉ
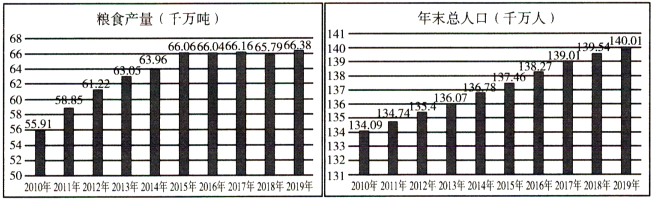
A.ЮвЙњСИЪГФъВњСПгыФъФЉзмШЫПкОљж№ФъЕнді
B.2011ФъЮвЙњСИЪГФъВњСПЕФФъдіГЄТЪзюДѓ
C.2015ФъЉ2019ФъЮвЙњСИЪГФъВњСПЯрЖдЮШЖЈ
D.2015ФъЮвЙњШЫОљСИЪГФъВњСПДяЕНСЫзюИпЗх
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПВњСПЯрЭЌЕФЛњДВвЛКЭЛњДВЖўЩњВњЭЌвЛжжСуМўЃЌдквЛИіаЁЪБФкЩњВњГіЕФДЮЦЗЪ§ЗжБ№МЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЫќУЧЕФЗжВМСаЗжБ№ШчЯТЃК
ЃЌЫќУЧЕФЗжВМСаЗжБ№ШчЯТЃК
| 0 | 1 | 2 | 3 |
| 0.4 | 0.3 | 0.2 | 0.1 |
| 0 | 1 | 2 |
| 0.2 | 0.6 | 0.2 |
ЃЈ1ЃЉФФЬЈЛњДВИќКУЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉМЧ![]() БэЪО
БэЪО![]() ЬЈЛњДВ
ЬЈЛњДВ![]() аЁЪБФкЙВЩњВњГіЕФДЮЦЗМўЪ§ЃЌЧѓ
аЁЪБФкЙВЩњВњГіЕФДЮЦЗМўЪ§ЃЌЧѓ![]() ЕФЗжВМСа.
ЕФЗжВМСа.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌGHЪЧЖЋЮїЗНЯђЕФЙЋТЗББВрЕФБпдЕЯпЃЌФГЙЋЫОзМБИдкGHЩЯЕФвЛЕуBЕФе§ББЗНЯђЕФAДІНЈЩшвЛВжПтЃЌЩш![]() ЃЌВЂдкЙЋТЗББВрНЈдьБпГЄЮЊ
ЃЌВЂдкЙЋТЗББВрНЈдьБпГЄЮЊ![]() ЕФе§ЗНаЮЮоЖЅжазЊеОCDEFЃЈЦфжаEFдкGHЩЯЃЉЃЌЯжДгВжПтAЯђGHКЭжазЊеОЗжБ№аоСНЬѕЕРТЗAB,AC,вбжЊAB=AC+1ЃЌЧв
ЕФе§ЗНаЮЮоЖЅжазЊеОCDEFЃЈЦфжаEFдкGHЩЯЃЉЃЌЯжДгВжПтAЯђGHКЭжазЊеОЗжБ№аоСНЬѕЕРТЗAB,AC,вбжЊAB=AC+1ЃЌЧв![]() .
.
ЃЈ1ЃЉЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§НтЮіЪНЃЌВЂЧѓГіЖЈвхгђЃЛ
ЕФКЏЪ§НтЮіЪНЃЌВЂЧѓГіЖЈвхгђЃЛ
ЃЈ2ЃЉШчЙћжазЊеОЫФЖТЮЇЧНдьМлЮЊ10ЭђдЊ/km,СНЬѕЕРТЗдьМлЮЊ30ЭђдЊ/km,ЮЪЃК![]() ШЁКЮжЕЪБЃЌИУЙЋЫОНЈЩшжазЊеОЮЇЧНКЭСНЬѕЕРТЗзмдьМлMзюЕЭ.
ШЁКЮжЕЪБЃЌИУЙЋЫОНЈЩшжазЊеОЮЇЧНКЭСНЬѕЕРТЗзмдьМлMзюЕЭ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЎ
ЃЎ
ЃЈЂёЃЉМЧ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌКуга
ЪБЃЌКуга![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂђЃЉШє![]() ЃЌЧѓжЄЃКЖдШЮвт
ЃЌЧѓжЄЃКЖдШЮвт![]() ЃЌ
ЃЌ![]() гы
гы![]() дк
дк![]() ЩЯгаЮЈвЛЙЋЙВЕуЃЎ
ЩЯгаЮЈвЛЙЋЙВЕуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЗжБ№ЮЊЭждВ
ЗжБ№ЮЊЭждВ![]() ЕФзѓЁЂгвНЙЕуЃЌ
ЕФзѓЁЂгвНЙЕуЃЌ![]() ЮЊИУЭждВЕФвЛЬѕДЙжБгк
ЮЊИУЭждВЕФвЛЬѕДЙжБгк![]() жсЕФЖЏЯвЃЌжБЯп
жсЕФЖЏЯвЃЌжБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() гыжБЯп
гыжБЯп![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() .
.
ЃЈ1ЃЉжЄУїЃКЕу![]() КудкЭждВ
КудкЭждВ![]() ЩЯ.
ЩЯ.
ЃЈ2ЃЉЩшжБЯп![]() гыЭждВ
гыЭждВ![]() жЛгавЛИіЙЋЙВЕу
жЛгавЛИіЙЋЙВЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() гыжБЯп
гыжБЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌдкЦНУцФкЪЧЗёДцдкЖЈЕу
ЃЌдкЦНУцФкЪЧЗёДцдкЖЈЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() КуГЩСЂЃПШєДцдкЃЌЧѓГіИУЕузјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
КуГЩСЂЃПШєДцдкЃЌЧѓГіИУЕузјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() дкЖЈвхгђФкгаСНИіВЛЭЌЕФМЋжЕЕу.
дкЖЈвхгђФкгаСНИіВЛЭЌЕФМЋжЕЕу.
ЃЈ1ЃЉЧѓ![]() ЕФШЁжЕЗЖЮЇ;
ЕФШЁжЕЗЖЮЇ;
ЃЈ2ЃЉЩшСНИіМЋжЕЕуЗжБ№ЮЊЃК![]() ЃЌ
ЃЌ![]() ЃЌжЄЃК
ЃЌжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§РтжљABCЉA1B1C1жаЃЌВрУцBB1C1CЮЊСтаЮЃЌ![]() ЃЎ
ЃЎ
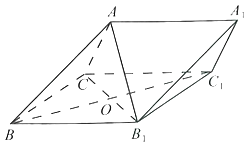
ЃЈ1ЃЉЧѓжЄЃКB1CЁЭABЃЛ
ЃЈ2ЃЉШєЁЯCBB1ЃН60ЁуЃЌACЃНBCЃЌЧвЕуAдкВрУцBB1C1CЩЯЕФЭЖгАЮЊЕуOЃЌЧѓЖўУцНЧBЉAA1ЉCЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНёФъЃЌаТаЭЙкзДВЁЖОРДЪЦазУЭЃЌРЯАйаевЛЪБМфЁАЬИЖОЩЋБфЁБЃЌНќРДЃЌгаЙиКШАзОЦПЩвддЄЗРВЁЖОЕФЫЕЗЈвЛжБдкУёМфСїДЋЃЌИќгаШЫФУГіЁАвНЁБзжЕФЗБЬхзжЁАсtЁБНјааНтЖСЮЊЃКвНжЮЮСвпвЊКШОЦЃЌЮЊСЫЕїВщКШАзОЦЪЧЗёгажњгкдЄЗРВЁЖОЃЌЮвУЧЕїВщСЫ1000ШЫЕФКШОЦЩњЛюЯАЙпгызюжеЪЧЗёЕУВЁНјааСЫЭГМЦЃЌБэИёШчЯТЃК
УПжмКШОЦСПЃЈСНЃЉ |
|
|
|
|
|
ШЫЪ§ | 100 | 300 | 450 | 100 |
|
ЙцЖЈЃКЂйУПжмКШОЦСПДяЕН4СНЕФНаГЃКШОЦШЫЃЌЗДжЎНаВЛГЃКШОЦШЫЃЛ
ЂкУПжмКШОЦСПДяЕН8СНЕФНагаОЦёЋЕФШЫ.
ЃЈ1ЃЉЧѓ![]() жЕЃЌДгУПжмКШОЦСПДяЕН6СНЕФШЫжаАДееЗжВуГщбљбЁГі6ШЫЃЌдйДгет6ШЫжабЁГі2ШЫЃЌЧѓет2ШЫжаЮогаОЦёЋЕФШЫЕФИХТЪЃЛ
жЕЃЌДгУПжмКШОЦСПДяЕН6СНЕФШЫжаАДееЗжВуГщбљбЁГі6ШЫЃЌдйДгет6ШЫжабЁГі2ШЫЃЌЧѓет2ШЫжаЮогаОЦёЋЕФШЫЕФИХТЪЃЛ
ЃЈ2ЃЉЧыЭЈЙ§ЩЯЪіБэИёжаЕФЭГМЦЪ§ОнЃЌЬюаДЭъЯТУцЕФ![]() СаСЊБэЃЌВЂЭЈЙ§МЦЫуХаЖЯЪЧЗёФмдкЗИДэЮѓЕФИХТЪВЛГЌЙ§0.1ЕФЧАЬсЯТШЯЮЊЪЧЗёЕУВЁгыЪЧЗёГЃКШОЦгаЙиЃПВЂЖдУёМфСїДЋЕФЫЕЗЈзіГіФуЕФХаЖЯ.
СаСЊБэЃЌВЂЭЈЙ§МЦЫуХаЖЯЪЧЗёФмдкЗИДэЮѓЕФИХТЪВЛГЌЙ§0.1ЕФЧАЬсЯТШЯЮЊЪЧЗёЕУВЁгыЪЧЗёГЃКШОЦгаЙиЃПВЂЖдУёМфСїДЋЕФЫЕЗЈзіГіФуЕФХаЖЯ.
ГЃКШОЦ | ВЛГЃКШОЦ | КЯМЦ | |
ЕУВЁ | |||
ВЛЕУВЁ | 250 | 650 | |
КЯМЦ |
ВЮПМЙЋЪНЃК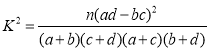 ЃЌЦфжа
ЃЌЦфжа![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com