
【题目】已知函数![]() (
(![]() 是自然对数的底数),
是自然对数的底数), ![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求![]() 的单调区间;
的单调区间;
(3)设![]() ,其中
,其中![]() 为
为![]() 的导函数,证明:对任意
的导函数,证明:对任意![]() .
.
科目:高中数学 来源: 题型:
【题目】空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2017年1月某日某省x个监测点数据统计如下:
空气污染指数 (单位:μg/m3) |
|
|
|
|
监测点个数 | 15 | 40 | y | 10 |
(1)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的发展,微信越来越成为人们交流的一种方式,某机构对使用微信交流的态度进行调查,随机调查了50人,他们年龄的频数分布及对使用微信交流赞成人数如表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)由以上统计数据填写下面![]() 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若对年龄分别在![]() ,
, ![]() 的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
参考公式: ![]() ,其中
,其中![]()
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某物体一天中的温度![]() 是时间
是时间![]() 的函数,已知
的函数,已知![]() ,其中温度的单位是
,其中温度的单位是![]() ,时间的单位是小时,规定中午12:00相应的
,时间的单位是小时,规定中午12:00相应的![]() ,中午12:00以后相应的
,中午12:00以后相应的![]() 取正数,中午12:00以前相应的
取正数,中午12:00以前相应的![]() 取负数(例如早上8:00相应的
取负数(例如早上8:00相应的![]() ,下午16:00相应的
,下午16:00相应的![]() ),若测得该物体在中午12:00的温度为
),若测得该物体在中午12:00的温度为![]() ,在下午13:00的温度为
,在下午13:00的温度为![]() ,且已知该物体的温度在早上8:00与下午16:00有相同的变化率.
,且已知该物体的温度在早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度![]() 关于时间
关于时间![]() 的函数关系式;
的函数关系式;
(2)该物体在上午10:00至下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查高一新生中女生的体重情况,校卫生室随机选20名女生作为样本,测量她们的体重(单位:kg),获得的所有数据按照区间![]() ,
, ![]() ,
, ![]() ,
, ![]() 进行分组,得到频率分布直方图如图所示,已知样本中体重在区间
进行分组,得到频率分布直方图如图所示,已知样本中体重在区间![]() 上的女生数与体重在区间
上的女生数与体重在区间![]() 上的女生数之比为
上的女生数之比为![]() .
.

(1)求![]() 的值;
的值;
(2)从样本中体重在区间![]() 上的女生中随机抽取两人,求体重在区间
上的女生中随机抽取两人,求体重在区间![]() 上的女生至少有一人被抽中的概率.
上的女生至少有一人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了解高中学生的性别和喜爱打篮球是否有关,对50名高中学生进行了问卷调查,得到如下列联表:
喜爱打篮球 | 不喜欢打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 |
已知在这50人中随机抽取1人,抽到喜欢打篮球的学生的概率为![]() .
.
(1)请将上述列联表补充完整;
(2)判断是否有99.5%的把握认为喜欢打篮球与性别有关?
附: 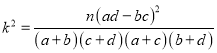
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com