[题目]已知P为椭圆 =1上的一个点.M.N分别为圆(x+3)2+y2=1和圆2+y2=4上的点.则|PM|+|PN|的最小值为．题目和参考答案——青夏教育精英家教网—

【题目】已知P为椭圆 =1上的一个点，M，N分别为圆（x+3）2+y2=1和圆（x﹣3）2+y2=4上的点，则|PM|+|PN|的最小值为．

【答案】7
【解析】解：由椭圆 =1可得a=5，b=4，c=3，因此焦点分别为：F1（﹣3，0），F2（3，0）． |PF1|+|PF2|=2a=10．
圆（x+3）2+y2=1的圆心与半径分别为：F1（﹣3，0），r1=1；
圆（x﹣3）2+y2=4的圆心与半径分别为：F2（3，0），r2=2．
∵|PM|+r1≥|PF1|，|PN|+r2≥|PF2|．
∴|PM|+|PN|≥|PF1|+|PF2|﹣1﹣2=7．
故答案为：7．
由椭圆 =1可得焦点分别为：F1（﹣3，0），F2（3，0）．|PF1|+|PF2|=2a．圆（x+3）2+y2=1的圆心与半径分别为：F1 ， r1=1；圆（x﹣3）2+y2=4的圆心与半径分别为：F2 ， r2=2．利用|PM|+r1≥|PF1|，|PN|+r2≥|PF2|．即可得出．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．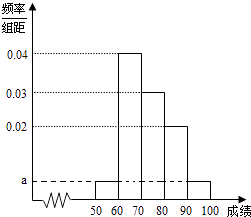
（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；
（3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求数学成绩在[50，90）之外的人数．

分数段	[50，60）	[60，70）	[70，80）	[80，90）
x：y	1：1	2：1	3：4	4：5

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在Rt△ABC中，∠ACB＝，AC＝3， BC＝2，P是△ABC内的一点．

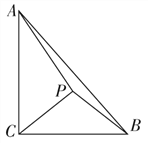
（1）若P是等腰直角三角形PBC的直角顶点，求PA的长；

（2）若∠BPC＝，设∠PCB＝θ，求△PBC的面积S(θ)的解析式，并求S(θ)的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知幂函数在（0，+∞）上为增函数，g（x）=f（x）+2
（1）求m的值，并确定f（x）的解析式；
（2）对于任意x∈[1，2]，都存在x1 ， x2∈[1，2]，使得f（x）≤f（x1），g（x）≤g（x2），若f（x1）=g（x2），求实数t的值；
（3）若2xh（2x）+λh（x）≥0对于一切x∈[1，2]成成立，求实数λ的取值范围．