
【题目】已知![]() 为抛物线
为抛物线![]() :
:![]() 的焦点,过
的焦点,过![]() 的动直线交抛物线
的动直线交抛物线![]() 于
于![]() ,
,![]() 两点.当直线与
两点.当直线与![]() 轴垂直时,
轴垂直时,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 的斜率为1且与抛物线的准线
的斜率为1且与抛物线的准线![]() 相交于点
相交于点![]() ,抛物线
,抛物线![]() 上存在点
上存在点![]() 使得直线
使得直线![]() ,
,![]() ,
,![]() 的斜率成等差数列,求点
的斜率成等差数列,求点![]() 的坐标.
的坐标.
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:
【题目】定义变换![]() 将平面内的点
将平面内的点![]() 变换到平面内的点
变换到平面内的点![]() ;若曲线
;若曲线![]() 经变换
经变换![]() 后得到曲线
后得到曲线![]() ,曲线
,曲线![]() 经变换
经变换![]() 后得到曲线
后得到曲线![]() ,…,依次类推,曲线
,…,依次类推,曲线![]() 经变换
经变换![]() 后得到曲线
后得到曲线![]() ,当
,当![]() 时,记曲线
时,记曲线![]() 与
与![]() 、
、![]() 轴正半轴的交点为
轴正半轴的交点为![]() 和
和![]() ,某同学研究后认为曲线
,某同学研究后认为曲线![]() 具有如下性质:①对任意的
具有如下性质:①对任意的![]() ,曲线
,曲线![]() 都关于原点对称;②对任意的
都关于原点对称;②对任意的![]() ,曲线
,曲线![]() 恒过点
恒过点![]() ;③对任意的
;③对任意的![]() ,曲线
,曲线![]() 均在矩形
均在矩形![]() (含边界)的内部,其中
(含边界)的内部,其中![]() 的坐标为
的坐标为![]() ;④记矩形
;④记矩形![]() 的面积为
的面积为![]() ,则
,则![]() ;其中所有正确结论的序号是_______.
;其中所有正确结论的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c.满足2acosC+bcosC+ccosB=0.
(Ⅰ)求角C的大小;
(Ⅱ)若a=2,△ABC的面积为![]() ,求C的大小。
,求C的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过点
过点![]() ,并且与圆
,并且与圆![]() :
:![]() 相外切,设动圆的圆心
相外切,设动圆的圆心![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过动点![]() 作直线与曲线
作直线与曲线![]() 交于
交于![]() 两点,当
两点,当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的值;
的值;
(3)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,设直线
两点,设直线![]() :
:![]() ,点
,点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,求证:直线
,求证:直线![]() 经过定点,并求出该定点的坐标.
经过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,网购已经逐渐融入了人们的生活.在家里面不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,如果近的话当天买当天就能送到,或者第二天就能送到,所以网购是非常方便的购物方式.某公司组织统计了近五年来该公司网购的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年)的数据,列表如下:
(单位:年)的数据,列表如下:
| 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
(1)依据表中给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).(若
并加以说明(计算结果精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式
 ,参考数据
,参考数据![]() .
.
(2)建立![]() 关于
关于![]() 的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
(参考公式:
 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且抛物线
,且抛物线![]() 的焦点恰好是椭圆
的焦点恰好是椭圆![]() 的一个焦点.
的一个焦点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 满足
满足![]() (
(![]() 为坐标原点),求四边形
为坐标原点),求四边形![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: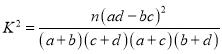
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com