证明:(I)由S
n+2n=2a
n得 S
n=2a
n-2n
当n∈N
*时,S
n=2a
n-2n,①
当n=1 时,S
1=2a
1-2,则a
1=2,
则当n≥2,n∈N
*时,S
n-1=2a
n-1-2(n-1).②
①-②,得a
n=2a
n-2a
n-1-2,即a
n=2a
n-1+2,∴a
n+2=2(a
n-1+2)
∴数列{a
n+2}是以a
1+2为首项,以2为公比的等比数列.
∴a
n+2=4•2
n-1,
∴a
n=2
n+1-2.
(Ⅱ)由b
n=log
2(a
n+2)=log22n+1=n+1,
∴
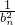
=
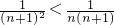
=

∴
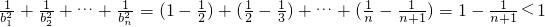
.
分析:(I)由S
n+2n=2a
n得S
n=2a
n-2n,再写一式,两式相减,即可证数列{a
n+2}是以a
1+2为首项,以2为公比的等比数列,从而可求数列{a
n}的通项公式a
n;
(Ⅱ)由b
n=log
2(a
n+2)=log22n+1=n+1,则
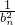
=
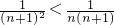
=

,由此可证结论.
点评:本题考查数列递推式,考查等比数列的证明,考查数列的通项,考查不等式的证明,确定数列的通项,正确放缩是关键.

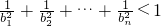 .
.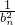 =
=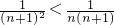 =
=
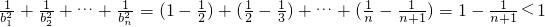 .
.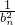 =
=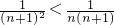 =
= ,由此可证结论.
,由此可证结论.

 阅读快车系列答案
阅读快车系列答案