
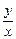 的最大值和最小值;(2)y-x的最小值;(3)x2+y2的最大值和最小值.
的最大值和最小值;(2)y-x的最小值;(3)x2+y2的最大值和最小值.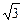 ,kmin=-
,kmin=-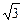 . (2)(y-x)min=-2-
. (2)(y-x)min=-2-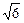 .
.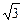
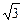 为半径的圆.
为半径的圆.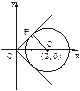
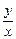 =k,即y=kx,由圆心(2,0)到y=kx的距离为半径时直线与圆相切,斜率取得最大、最小值.由
=k,即y=kx,由圆心(2,0)到y=kx的距离为半径时直线与圆相切,斜率取得最大、最小值.由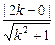 =
=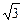 ,解得k2=3.所以kmax=
,解得k2=3.所以kmax=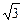 ,kmin=-
,kmin=-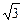 .
.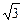 ,∠POC=60°,直线OP的倾斜角为60°,直线OP′的倾斜角为120°解之)
,∠POC=60°,直线OP的倾斜角为60°,直线OP′的倾斜角为120°解之)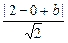 =
=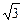 ,即b=-2±
,即b=-2±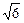 ,故(y-x)min=-2-
,故(y-x)min=-2-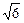 .
.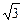 ,(x2+y2)min=|OB|=2-
,(x2+y2)min=|OB|=2-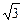 .
.

科目:高中数学 来源:不详 题型:解答题
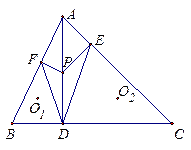
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
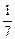 B.-1<t<
B.-1<t< C.-
C.-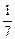 <t<1 D.1<t<2
<t<1 D.1<t<2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com