
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0). 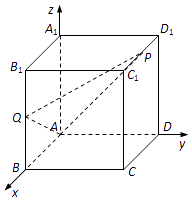
(1)若 ![]() ,求AP与AQ所成角的余弦值;
,求AP与AQ所成角的余弦值;
(2)若直线AA1与平面APQ所成的角为45°,求实数λ的值.
【答案】
(1)解:以 ![]() 为正交基底,建立如图所示空
为正交基底,建立如图所示空
间直角坐标系A﹣xyz.
因为 ![]() ,
, ![]() ,
,
所以 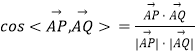 =
= ![]() .
.
所以AP与AQ所成角的余弦值为 ![]()
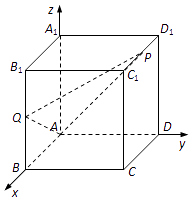
(2)解:由题意可知, ![]() ,
, ![]() .
.
设平面APQ的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 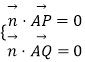 即
即 ![]()
令z=﹣2,则x=2λ,y=2﹣λ.
所以 ![]() =(2λ,2﹣λ,﹣2).
=(2λ,2﹣λ,﹣2).
又因为直线AA1与平面APQ所成角为45°,
所以|cos< ![]() ,
, ![]() >|=
>|= 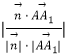 =
= ![]() ,
,
可得5λ2﹣4λ=0,又因为λ≠0,所以 ![]() .
.
【解析】(1)以 ![]() 为正交基底,建立如图所示空间直角坐标系A﹣xyz.求出
为正交基底,建立如图所示空间直角坐标系A﹣xyz.求出 ![]() ,
, ![]() ,利用数量积求解AP与AQ所成角的余弦值.(2)
,利用数量积求解AP与AQ所成角的余弦值.(2) ![]() ,
, ![]() .求出平面APQ的法向量,利用空间向量的数量积求解即可.
.求出平面APQ的法向量,利用空间向量的数量积求解即可.
【考点精析】认真审题,首先需要了解空间角的异面直线所成的角(已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则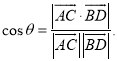 ).
).


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三 年级一班至六班进行了“本届奥运会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了50人,具体的调查结果如表:
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 5 | 9 | 11 | 9 | 7 | 9 |
满意人数 | 4 | 7 | 8 | 5 | 6 | 6 |
(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为ξ,求随机变量ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|4x﹣a|+|4x+3|,g(x)=|x﹣1|﹣|2x|.
(1)解不等式g(x)>﹣3;
(2)若存在x1∈R,也存在x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,焦点到相应准线的距离为1.
,焦点到相应准线的距离为1. 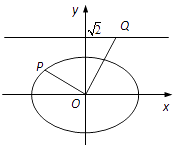
(1)求椭圆的标准方程;
(2)若P为椭圆上的一点,过点O作OP的垂线交直线 ![]() 于点Q,求
于点Q,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,已知第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,……,则此数列的前56项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,……,则此数列的前56项和为( )

A. 2060B. 2038C. 4084D. 4108
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个同学分別抛掷一枚质地均匀的骰子.
(1)求他们抛掷的骰子向上的点数之和是4的倍数的概率;
(2)求甲抛掷的骰子向上的点数不大于乙抛掷的骰子向上的点数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海南沿海某次超强台风过后,当地人民积极恢复生产,焊接工王师傅每天都很忙碌.一天他遇到了一个难题:如图所示,有一块扇形钢板,半径为![]() 米,圆心角
米,圆心角![]() ,施工要求按图中所画的那样,在钢板
,施工要求按图中所画的那样,在钢板![]() 上裁下一块平行四边形钢板
上裁下一块平行四边形钢板![]() ,要求使裁下的钢板面积最大.请你帮助王师傅解决此问题.连接
,要求使裁下的钢板面积最大.请你帮助王师傅解决此问题.连接![]() ,设
,设![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() .
.

(1)求线段![]() 的长度(用
的长度(用![]() 来表示);
来表示);
(2)求平行四边形![]() 面积的表达式(用
面积的表达式(用![]() 来表示);
来表示);
(3)为使平行四边形![]() 面积最大,
面积最大,![]() 等于何值?最大面积是多少?
等于何值?最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() (侧棱垂直于底面)中,
(侧棱垂直于底面)中,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() 使
使![]() 平面
平面![]() ?若存在,请确定点
?若存在,请确定点![]() 的位置;若不存在,也请说明理由.
的位置;若不存在,也请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( ) 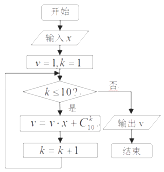
A.210﹣1
B.210
C.310﹣1
D.310
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com