
分析 (1)由所求圆与y轴相切,得到圆心的横坐标的绝对值为圆的半径,进而由圆心C的坐标和求出的半径写出圆的标准方程即可.
(2)假设存在满足题意的直线,方程为y=x+m,由直线与圆C相交,求出交点的坐标,由直线与圆的方程联立,消去y,根据根与系数的关系,结合OA⊥OB,求m的值即可.
解答 解:(1)∵圆心C的坐标为(1,-2),且所求圆与y轴相切,
∴圆的半径r|=1,
则所求圆的方程为(x-1)2+(y+2)2=1;
(2)设存在满足题意的直线,且此直线方程为y=x+m,
直线与圆C相交于A,B两点的坐标分别为(x1,y1),(x2,y2),
由OA⊥OB,得kOA•kOB=-1,即x1x2+y1y2=0;
由y=x+m与(x-1)2+(y+2)2=1,消去y得,
2x2+2(m+1)x+m2+4m+4=0,
∴x1+x2=-(m+1),x1x2=$\frac{1}{2}$(m2+4m+4)
又∵x1x2+y1y2=0,
y1=x1+m,y2=x2+m;
∴x1x2+(x1+m)(x2+m)=0,
即2x1x2+m(x1+x2)+m2=0;
∴m2+4m+4-m(m+1)+m2=0,
∴m2+3m+4=0
△<0,∴不存在满足题意的直线.
点评 此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,当直线与圆相切时,圆心到直线的距离等于圆的半径,其中根据题意得到圆心横坐标的绝对值为圆的半径是解本题的关键.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
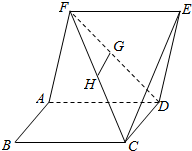 如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.
如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com