
【题目】学校高一数学考试后,对![]() 分(含
分(含![]() 分)以上的成绩进行统计,其頻率分布直方图如图所示,分数在
分)以上的成绩进行统计,其頻率分布直方图如图所示,分数在![]() 分的学生人数为
分的学生人数为![]() 人.
人.
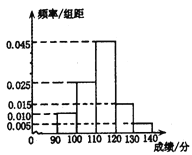
(1)求这所学校分数在![]() 分的学生人数;
分的学生人数;
(2)请根据频率发布直方图估计这所学校学生分数在![]() 分的学生的平均成绩;
分的学生的平均成绩;
(3)为进一步了解学生的学习情况,按分层抽样方法从分数在![]() 分和
分和![]() 分的学生中抽出
分的学生中抽出![]() 人,从抽出的学生中选出
人,从抽出的学生中选出![]() 人分别做问卷
人分别做问卷![]() 和问卷
和问卷![]() ,求
,求![]() 分的学生做问卷
分的学生做问卷![]() ,
, ![]() 分的学生做问卷
分的学生做问卷![]() 的概率.
的概率.
【答案】(1)200人;(2)113分;(3)![]() .
.
【解析】试题分析:(1)由分数在120~130分的学生人数为30人,且分数在120~130分频率为0.15,能求出分数在90~140分的学生人数.
(2)由频率分布直方图能估计这所学校学生分数在90~140分的学生的平均成绩.
(3)分数在90~100分的学生人数为20人,分数在120~130分的学生人数为30人,按照分层抽样方法抽出5人时,从分数在90~100分的学生抽出2人,记为A1,A2,从分数在![]() 分的学生抽出3人,记为B1,B2,B3,从抽取的5人中选出2人分别做问卷A和问卷B,利用列举法能求出90-100分的学生做问卷A,120-130分的学生做问卷B的概率.
分的学生抽出3人,记为B1,B2,B3,从抽取的5人中选出2人分别做问卷A和问卷B,利用列举法能求出90-100分的学生做问卷A,120-130分的学生做问卷B的概率.
试题解析:
(1)![]() 分数在
分数在![]() 分的学生人数为
分的学生人数为![]() 人,且分数在
人,且分数在![]() 分频率为
分频率为![]() ,
, ![]() 分数在
分数在![]() 分的学生人数为
分的学生人数为![]() 人.
人.
(2)估计这所学校学生分数在![]() 分的学生的平均成绩为
分的学生的平均成绩为
![]() 分.
分.
(3)因为分数在![]() 分的学生人数为
分的学生人数为![]() 人,分数在
人,分数在![]() 分的学生人数为
分的学生人数为![]() 人,所以按分层抽样方法抽出
人,所以按分层抽样方法抽出![]() 人时,分数在
人时,分数在![]() 分的学生抽出
分的学生抽出![]() 人,记为
人,记为![]() ,分数在
,分数在![]() 分的学生抽出
分的学生抽出![]() 人,记为
人,记为![]() .从抽出
.从抽出![]() 人中选出
人中选出![]() 人分别做问卷
人分别做问卷![]() 和问卷
和问卷![]() ,共有
,共有![]() 种情况,分别为
种情况,分别为![]() , 设事件
, 设事件![]() “
“![]() 分的学生做问卷
分的学生做问卷![]() ,
, ![]() 分的学生做问卷
分的学生做问卷![]() ”,则事件
”,则事件![]() 共有
共有![]() 种情况,分别为
种情况,分别为![]() ,
, ![]() ,即事件
,即事件![]() 的概率为
的概率为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板![]() ,其中顶点
,其中顶点![]() 、
、![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在
在![]() 上,
上, ![]() ,
, ![]() .设
.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
(1)用含![]() 的式子表示
的式子表示![]() ,
, ![]() 的长;
的长;
(2)试将![]() 表示为
表示为![]() 的函数;
的函数;
(3)求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有5张编号依次为1、2、3、4、5的卡片,这5 张卡片除号码外完全相同.现进行有放回的连续抽取2 次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求事件“取出卡片号码之和不小于7 或小于5”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() (
(![]() )的离心率是
)的离心率是![]() ,抛物线
,抛物线![]() :
:![]() 的焦点
的焦点![]() 是
是![]() 的一个顶点.
的一个顶点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是
是![]() 上的动点,且位于第一象限,
上的动点,且位于第一象限,![]() 在点
在点![]() 处的切线
处的切线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与过
与过![]() 且垂直于
且垂直于![]() 轴的直线交于点
轴的直线交于点![]() .
.
(i)求证:点![]() 在定直线上;
在定直线上;
(ii)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,记△
,记△![]() 的面积为
的面积为![]() ,△
,△![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值及取得最大值时点
的最大值及取得最大值时点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,
, ![]() 都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
(2)若![]() ,
, ![]() 都是从区间
都是从区间![]() 上任取的一个数,求
上任取的一个数,求![]() 成立的概率.
成立的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com