
【题目】已知圆C与圆C1:5x2+5y2﹣mx﹣16y+32=0外切于点P(![]() ),且与y轴相切.
),且与y轴相切.
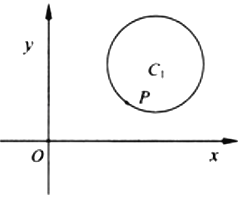
(1)求圆C的方程
(2)过点O作直线l1,l2分别交圆C于A、B两点,若l1,l2斜率之积为﹣2,求△ABC面积S的最大值
【答案】(1)(x﹣1)2+y2=1;(2)![]() .
.
【解析】
(1)根据P(![]() )在圆C1上,有
)在圆C1上,有![]() ,求得m=22,得
,求得m=22,得![]() ,C1P方程为4x﹣3y﹣4=0,设C(x0,y0)(x0>0),根据圆C与y轴相切和圆C与圆C1外切于P,建立方程组
,C1P方程为4x﹣3y﹣4=0,设C(x0,y0)(x0>0),根据圆C与y轴相切和圆C与圆C1外切于P,建立方程组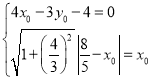 求解.
求解.
(2)根据题意设l1:y=kx,l2:y![]() x,由
x,由![]() ,消去y得(k2+1)x2+2x=0,解得x=0,
,消去y得(k2+1)x2+2x=0,解得x=0,![]() ,得到
,得到![]() ,同理可得
,同理可得 ,①当直线AB的斜率不存在时,易得
,①当直线AB的斜率不存在时,易得![]() ;②当直线AB的斜率存在时,直线AB的方程为
;②当直线AB的斜率存在时,直线AB的方程为![]() ,化简得
,化简得![]() ,直线AB恒过
,直线AB恒过![]() ,然后由
,然后由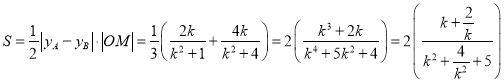 求解.
求解.
(1)∵P(![]() )在圆C1上,∴
)在圆C1上,∴![]() ,
,
解得m=22,
∴圆![]() ,得
,得![]() ,
,
可得C1P方程为4x﹣3y﹣4=0,
设C(x0,y0)(x0>0),
∵圆C与y轴相切,∴r=x0,
又圆C与圆C1外切于P,∴C在直线C1P上,且CP=r,
则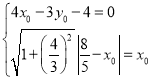 ,解得
,解得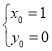 或
或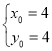 ,
,
∵圆C与圆C1外切,∴C(1,0),
∴圆C的方程为(x﹣1)2+y2=1;
(2)如图所示:
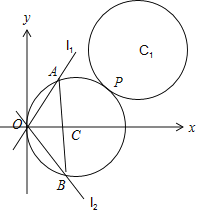
设直线l1的斜率为k(不妨设k>0),则直线l2的斜率为![]() ,
,
∴l1:y=kx,l2:y![]() x,
x,
由![]() ,消去y得(k2+1)x2+2x=0,
,消去y得(k2+1)x2+2x=0,
解得x=0,![]() ,∴
,∴![]() ,
,
以![]() 代k同理可得
代k同理可得 ,
,
①当直线AB的斜率不存在时,
由![]() ,得
,得![]() ,弦AB的长度为
,弦AB的长度为![]() ,
,![]() ;
;
②当直线AB的斜率存在时,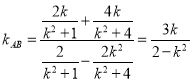 ,
,
∴直线AB的方程为![]() ,化简得
,化简得![]() ,
,
∴直线AB恒过![]() ,
,
∴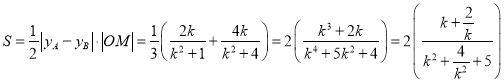 .
.
设![]() ,则
,则![]() ,
,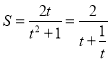 ,
,
设![]() ,
,![]() ,
,
∴f(t)在![]() 上单调增,得
上单调增,得![]() ,
,
∴![]() .
.
综上,△ABC面积S的最大值为![]() .
.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
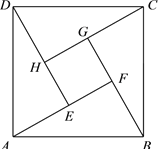
【题目】如图,四边形![]() 是某市中心一边长为
是某市中心一边长为![]() 百米的正方形地块的平面示意图. 现计划在该地块上划分四个完全相同的直角三角形(即
百米的正方形地块的平面示意图. 现计划在该地块上划分四个完全相同的直角三角形(即![]() 和
和![]() ),且在这四个直角三角形区域内进行绿化,中间的小正方形修建成市民健身广场,为了方便市民到达健身广场,拟修建
),且在这四个直角三角形区域内进行绿化,中间的小正方形修建成市民健身广场,为了方便市民到达健身广场,拟修建![]() 条路
条路![]()
![]()
![]()
![]() . 已知在直角三角形内进行绿化每1万平方米的费用为
. 已知在直角三角形内进行绿化每1万平方米的费用为![]() 元,中间小正方形修建广场每1万平方米的费用为
元,中间小正方形修建广场每1万平方米的费用为![]() 元,修路每1百米的费用为
元,修路每1百米的费用为![]() 元,其中
元,其中![]() 为正常数.设
为正常数.设![]() ,
,![]() .
.
(1)用![]() 表示该工程的总造价
表示该工程的总造价![]() ;
;
(2)当![]() 为何值时,该工程的总造价最低?
为何值时,该工程的总造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与直线
与直线![]() 分别与椭圆
分别与椭圆![]()
![]() 交于点
交于点![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 上一点
上一点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() ,设直线
,设直线![]() 与椭圆
与椭圆![]() 相较于
相较于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
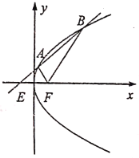
【题目】如图,已知F是抛物线C:![]() 的焦点,过E(﹣l,0)的直线
的焦点,过E(﹣l,0)的直线![]() 与抛物线分別交于A,B两点(点A,B在x轴的上方).
与抛物线分別交于A,B两点(点A,B在x轴的上方).
(1)设直线AF,BF的斜率分別为![]() ,
,![]() ,证明:
,证明:![]() ;
;
(2)若![]() ABF的面积为4,求直线
ABF的面积为4,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 作一条直线
作一条直线![]() 与其两条渐近线交于
与其两条渐近线交于![]() 两点,若
两点,若![]() 为等腰直角三角形,记双曲线的离心率为
为等腰直角三角形,记双曲线的离心率为![]() ,则
,则![]() ______________.
______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是
是![]() 上的偶函数,对于任意
上的偶函数,对于任意![]() ,都有
,都有![]() 成立,当
成立,当![]() ,且
,且![]() 时,都有
时,都有![]() ,给出下列命题,其中所有正确命题为( ).
,给出下列命题,其中所有正确命题为( ).
A.![]()
B.直线![]() 是函数
是函数![]() 的图象的一条对称轴
的图象的一条对称轴
C.函数![]() 在
在![]() 上为增函数
上为增函数
D.函数![]() 在
在![]() 上有四个零点
上有四个零点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com