练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在一次模拟考试后，从高三某班随机抽取了20位学生的数学成绩，其分布如下：

    分组

    [90，100]

    [100，110）

    [110，120）

    [120，130）

    [130，140）

    [140，150）

    频数

    1

    2

    6

    7

    3

    1

    分数在130分（包括130分）以上者为优秀，据此估计该班的优秀率约为（　　）
    A.10%
    B.20%
    C.30%
    D.40%

    【答案】B
    【解析】解：由表可知，优秀的人数为3+1=4，
    故分数在130分（包括130分）以上者为优秀，则优秀率为=20%，
    故据此估计该班的优秀率约20%，
    故选：B．
    【考点精析】通过灵活运用频率分布表，掌握第一步，求极差；第二步，决定组距与组数；第三步，确定分点，将数据分组；第四步，列频率分布表即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，点P到两点（0，﹣），（0，）的距离之和等于4，设点P的轨迹为C，直线y=kx+1与C交于A，B两点．
    （1）写出C的方程；
    （2）若⊥ ， 求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2012年“双节”期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/t）分成六段：（60，65），[65，70），[70，75），[80，85），[85，90）后得到如图的频率分布直方图．
    （1）某调查公司在采样中，用到的是什么抽样方法？
    （2）求这40辆小型车辆车速的众数和中位数的估计值．
    （3）若从车速在[60，70）的车辆中任抽取2辆，求车速在[65，70）的车辆至少有一辆的概率．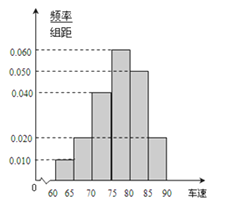

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥P﹣ABCD中，PA⊥底面ABCD，且PA=AB=AD=CD，AB∥CD，∠ADC=90°．
    （1）在侧棱PC上是否存在一点Q，使BQ∥平面PAD？证明你的结论；
    （2）求证：平面PBC⊥平面PCD；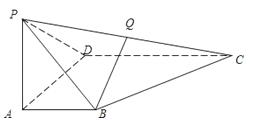

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列函数中，在其定义域内既是奇函数又是减函数的是（ ）
    A.y=x3 ， x∈R
    B.y=sinx，x∈R
    C.y=﹣x，x∈R
    D.y=（ ）x ， x∈R

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解某校今年准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第2小组的频数为12，则报考飞行员的总人数是 ．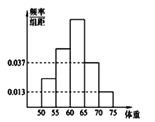

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=ax2﹣（a+1）x+1．
    （1）若不等式f（x）＜mx的解集为{x|1＜x＜2}，求实数a、m的值；
    （2）解不等式f（x）＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从高三学生中抽取50名同学参加数学竞赛，成绩的分组及各组的频数如下（单位：分）：
    [40，50），2；[50，60），3；[60，70），10；[70，80），15；[80，90），12；[90，100），8．
    （1）列出样本的频率分布表；
    （2）画出频率分布直方图和频率分布折线图；
    （3）估计成绩在[60，90）分的学生比例；
    （4）估计成绩在85分以下的学生比例．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱锥S﹣ABC中，AB⊥BC，AB=BC= ，SA=SC=2，二面角S﹣AC﹣B的余弦值是 ，若S、A、B、C都在同一球面上，则该球的表面积是 ．

    查看答案和解析>>

    同步练习册答案