
【题目】已知![]() .
.
(1)若![]() 是奇函数,求
是奇函数,求![]() 的值,并判断
的值,并判断![]() 的单调性(不用证明);
的单调性(不用证明);
(2)若函数![]() 在区间(0,1)上有两个不同的零点,求
在区间(0,1)上有两个不同的零点,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】下列说法: ①分类变量A与B的随机变量K2越大,说明“A与B有关系”的可信度越大.
②以模型y=cekx去拟合一组数据时,为了求出回归方程,设z=lny,将其变换后得到线性方程z=0.3x+4,则c,k的值分别是e4和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为y=a+bx中,b=1, ![]() =1,
=1, ![]() =3,
=3,
则a=1.正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
反感 | 10 | ||
不反感 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是 ![]() .
.
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
提示:可参考试卷第一页的公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,记
,记![]()
![]() .
.
(Ⅰ)求![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() ,求
,求 ![]() 的值;
的值;
(Ⅲ)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位得到
个单位得到![]() 的图象,若函数
的图象,若函数![]() 在
在![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥 ![]() 的底面为直角梯形,
的底面为直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 底面
底面 ![]() ,
, ![]() 为
为 ![]() 的中点.
的中点.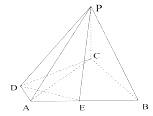
(Ⅰ)求证:平面 ![]() 平面
平面 ![]()
(Ⅱ)求直线 ![]() 与平面
与平面 ![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com