
【题目】如图,![]() 是底面边长为2,高为
是底面边长为2,高为![]() 的正三棱柱,经过AB的截面与上底面相交于PQ, 设
的正三棱柱,经过AB的截面与上底面相交于PQ, 设![]() .
.
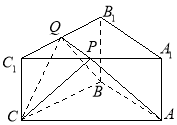
(Ⅰ)证明:![]() ;
;
(Ⅱ)当![]() 时,求点C到平面APQB的距离.
时,求点C到平面APQB的距离.
科目:高中数学 来源: 题型:
【题目】2017年天猫五一活动结束后,某地区研究人员为了研究该地区在五一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得概率分布直方图如图所示:记年龄在![]() ,
, ![]() ,
, ![]() 对应的小矩形的面积分别是
对应的小矩形的面积分别是![]() ,且
,且![]() .
.
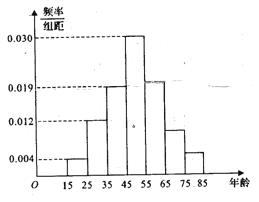
(1)以频率作为概率,若该地区五一消费超过3000元的有30000人,试估计该地区在五一活动中消费超过3000元且年龄在![]() 的人数;
的人数;
(2)计算在五一活动中消费超过3000元的消费者的平均年龄;
(3)若按照分层抽样,从年龄在![]() ,
, ![]() 的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在
的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,0),且圆C:x2+y2﹣6x+4y+4=0.
(Ⅰ)当直线![]() 过点P且与圆心C的距离为1时,求直线
过点P且与圆心C的距离为1时,求直线![]() 的方程;
的方程;
(Ⅱ)设过点P的直线与圆C交于A、B两点,若|AB|=4,求以线段AB为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() (
(![]() ).
).
(1)证明:直线![]() 过定点;
过定点;
(2)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,△
,△![]() 的面积为
的面积为![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的最小值,并求此时直线
的最小值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=![]() (m>0,n>0).
(m>0,n>0).
(1) 当m=n=1时,求证:f(x)不是奇函数;
(2) 设f(x)是奇函数,求m与n的值;
(3) 在(2)的条件下,求不等式f(f(x))+f![]() <0的解集.
<0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点分别为![]() ,且椭圆C过点P(3,2).
,且椭圆C过点P(3,2).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)与直线OP平行的直线交椭圆C于A,B两点,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选拔参加“全市高中数学竞赛”的选手,某中学举行了一次“数学竞赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() 分)作为样本(样本容量为
分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() 的数据).
的数据).
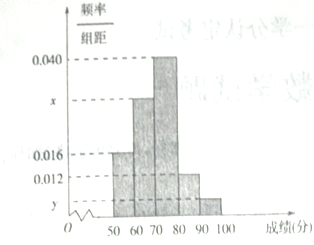
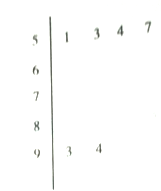
(1)求样本容![]() 和频率分布直方图中
和频率分布直方图中![]() 的值并求出抽取学生的平均分;
的值并求出抽取学生的平均分;
(2)在选取的样本中,从竞赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生中随机抽取
分)的学生中随机抽取![]() 名学生参加“全市中数学竞赛”求所抽取的
名学生参加“全市中数学竞赛”求所抽取的![]() 名学生中至少有一人得分在
名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
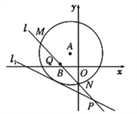
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com