
【题目】从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸出的球中有红球(不放回),则试验结束.
(1)求第一次试验恰摸到一个红球和一个白球概率;
(2)记试验次数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【答案】(1)![]() ;(2)
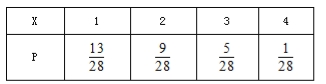
;(2)![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 |
|
|
|
|
|
![]()
【解析】
试题分析:(1)由题意知,袋子中共有8个球,记“第一次试验恰摸到一个红球和一个白球”为事件A,则根据古典概型计算公式,得![]() .
.
(2)由题意知,每次试验中不放回地摸出两个球,直到摸出的球中有红球,因为袋中只有两个红球,所以最多需要进行四次试验,第一次试验的结果可能有“一个红球一个白球”或“两个红球”,第二次试验要在第一次试验没有出红球情况下进行,则袋中剩下4个白球和2个红球,结果可能为“一个红球一个白球”或“两个红球”,同理第三次试验要在前两次没有出现红球下进行,则袋中剩下2个白球和2个红球,结果能为“一个红球一个白球”或“两个红球”,第四次试验要在前三次试验没有出现红球下进行,则袋中只剩下2个红球,结果为“两个红球”,所以![]() 的值为1、2、3、4,根据古典概型的计算公式,得
的值为1、2、3、4,根据古典概型的计算公式,得![]() ,
,![]() ,
,![]() ,
,![]() ,从而可列出
,从而可列出![]() 的分布列,并求出其数学期望
的分布列,并求出其数学期望![]() .
.
试题解析:(1)![]()
(2)由题意可知![]() 的值分别为1、2、3、4,则
的值分别为1、2、3、4,则![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() 的分布列为
的分布列为
![]() 的数学期望
的数学期望![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足:Sn= ![]() (an﹣1)(a为常数,且a≠0,a≠1);
(an﹣1)(a为常数,且a≠0,a≠1);
(1)求{an}的通项公式;
(2)设bn= ![]() +1,若数列{bn}为等比数列,求a的值;
+1,若数列{bn}为等比数列,求a的值;
(3)若数列{bn}是(2)中的等比数列,数列cn=(n﹣1)bn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换 得到曲线
得到曲线![]() .(1)求曲线
.(1)求曲线![]() 的普通方程;(2)若点
的普通方程;(2)若点![]() 在曲线
在曲线![]() 上,点
上,点![]()
![]() ,当点
,当点![]() 在曲线
在曲线![]() 上运动时,求
上运动时,求![]() 中点
中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=a﹣ ![]() ,
,
(1)若x∈[ ![]() ,+∞),①判断函数g(x)=f(x)﹣2x的单调性并加以证明;②如果f(x)≤2x恒成立,求a的取值范围;
,+∞),①判断函数g(x)=f(x)﹣2x的单调性并加以证明;②如果f(x)≤2x恒成立,求a的取值范围;
(2)若总存在m,n使得当x∈[m,n]时,恰有f(x)∈[2m,2n],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|﹣2|x﹣1|.
(1)解不等式f(x)≥﹣2;
(2)对任意x∈R,都有f(x)≤x﹣a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c且b=c,∠A的平分线为AD,若 ![]() =m
=m ![]()
![]() .
.
(1)当m=2时,求cosA
(2)当 ![]() ∈(1,
∈(1, ![]() )时,求实数m的取值范围.
)时,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且 ![]() ,∠AOQ=α,α∈[0,π). (Ⅰ)若点Q的坐标是
,∠AOQ=α,α∈[0,π). (Ⅰ)若点Q的坐标是 ![]() ,求
,求 ![]() 的值;
的值;
(Ⅱ)设函数 ![]() ,求f(α)的值域.
,求f(α)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com