
【题目】求具有如下性质的质数![]() 的最大值:存在1,2,
的最大值:存在1,2,![]() ,
,![]() 的两个排列(可以相同)
的两个排列(可以相同)![]() 与
与![]() ,使
,使![]() 被
被![]() 除所得的余数互不相同.
除所得的余数互不相同.
【答案】2
【解析】
先证明引理.
引理(威尔逊定理)对任何质数![]() ,有
,有![]() , ①
, ①
引理的证明:当![]() 时,式①显然成立.
时,式①显然成立.
当![]() 时,我们证明:对任何
时,我们证明:对任何![]() ,必存在
,必存在![]() ,使
,使![]() .
.
实际上,对![]() ,有
,有![]() .
.
从而,![]() 构成模
构成模![]() 的完系.
的完系.
于是,必存在![]() ,使
,使![]() ,
,
显然![]() ,否则
,否则![]() ,矛盾
,矛盾
此外,如![]() ,则由
,则由![]() ,得
,得![]() ,与
,与![]() 矛盾.
矛盾.
如果![]() ,则由
,则由![]() ,得
,得![]() ,与
,与![]() 矛盾.
矛盾.
如果![]() ,由
,由![]() ,得
,得![]() ,
,
所以,![]() ,但
,但![]() 矛盾.
矛盾.
因此,![]() ,且
,且![]() .
.
由此可知,乘积![]() 的各个因数可以配成
的各个因数可以配成![]() 对,每对中两个数的积模
对,每对中两个数的积模![]() 的余数为1.
的余数为1.
从而,![]() .
.
所以,![]() .
.
现在解决原题.
不妨设![]() ,并设
,并设![]() .
.
若![]() ,此时,
,此时,![]() .
.
又![]() 被
被![]() 除的余数互不相同.
除的余数互不相同.
所以, ![]() 被
被![]() 除的余数分别为
除的余数分别为![]() .
.
则![]() .
.
但另一方面,![]() 与
与![]() 是
是![]() 的两个排列,
的两个排列,
所以![]()
![]() ,
,
于是,![]() . ②
. ②
若![]() ,则与式②矛盾,所以,
,则与式②矛盾,所以,![]() ,
,
又当![]() 时,令
时,令![]()
此时,![]() ,
,![]() .
.
所以,![]() 条件,故
条件,故![]() .
.


科目:高中数学 来源: 题型:
【题目】我市为改善空气环境质量,控制大气污染,政府相应出台了多项改善环境的措施.其中一项是为了减少燃油汽车对大气环境污染.从2018年起大力推广使用新能源汽车,鼓励市民如果需要购车,可优先考虑选用新能源汽车.政府对购买使用新能源汽车进行购物补贴,同时为了地方经济发展,对购买本市企业生产的新能源汽车比购买外地企业生产的新能源汽车补贴高.所以市民对购买使用本市企业生产的新能源汽车的满意度也相应有所提高.有关部门随机抽取本市本年度内购买新能源汽车的![]() 户,其中有
户,其中有![]() 户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行.满分
户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行.满分![]() 分,将分数按照
分,将分数按照![]() 分成5组,得如下频率分布直方图.
分成5组,得如下频率分布直方图.
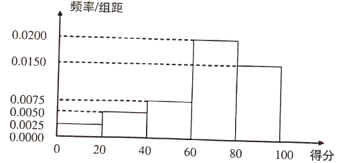
(1)若本次随机抽取的样本数据中购买使用本市企业生产的新能源汽车的用户中有![]() 户满意度得分不少于
户满意度得分不少于![]() 分,把得分不少于
分,把得分不少于![]() 分为满意.根据提供的条件数据,完成下面的列联表.
分为满意.根据提供的条件数据,完成下面的列联表.
满意 | 不满意 | 总计 | |
购本市企业生产的新能源汽车户数 | |||
购外地企业生产的新能源汽车户数 | |||
总计 |
并判断是否有![]() 的把握认为购买使用新能源汽车的满意度与产地有关?
的把握认为购买使用新能源汽车的满意度与产地有关?
(2)把满意度得分少于![]() 分的用户很不满意用户,在很不满意的用户中有
分的用户很不满意用户,在很不满意的用户中有![]() 户购买使用本市企业生产的新能源汽车,其他是购买外地产的.现在从样本中很不满意的用户中随机抽取
户购买使用本市企业生产的新能源汽车,其他是购买外地产的.现在从样本中很不满意的用户中随机抽取![]() 户进行了解很不满意的具体原因,求这
户进行了解很不满意的具体原因,求这![]() 户恰好是一户购买本市企业产的,另一户是购买外地企业产的概率.
户恰好是一户购买本市企业产的,另一户是购买外地企业产的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() ,
,![]() 为常数,且
为常数,且![]() 是函数
是函数![]() 的一个极值点.
的一个极值点.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若函数![]() ,
,![]() ,求
,求![]() 的单调区间;
的单调区间;
(Ⅲ) 过点![]() 可作曲线
可作曲线![]() 的三条切线,求
的三条切线,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体的![]() 个顶点,
个顶点,![]() 个侧面(底面)的中心及体的中心共
个侧面(底面)的中心及体的中心共![]() 个点中,若由两两不同的且不共线的
个点中,若由两两不同的且不共线的![]() 个点构成的平面与由另外
个点构成的平面与由另外![]() 个不同点构成的直线垂直,则称这
个不同点构成的直线垂直,则称这![]() 个点为“正交
个点为“正交![]() 点组”,那么,由这
点组”,那么,由这![]() 个点形成的正交
个点形成的正交![]() 点组的总个数为( )
点组的总个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 是函数
是函数![]() 的导函数,则
的导函数,则![]() 的图象大致是( )
的图象大致是( )
A. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/8f50d3dfba9b485fac00e42a95909498.png] B. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/74ae44978a70424c961e850ed79072da.png]
C. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/2f113f7ec5294ba0bbd1f66b13f3e152.png] D. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/dbaa9025ccdb497380b769e5396c4c19.png]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,以![]() 为概率的事件是( )
为概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com