
分析 先求出基本事件总数n=$8×2+{A}_{2}^{2}$=18,再利用列举法求出甲数小于乙数包含的基本基本事件,由此能求出甲数大于乙数的概率.
解答 解:甲乙两人从1,2,3,…,10中各任取一数(不重复),甲取到的数是5的倍数,
基本事件总数n=$8×2+{A}_{2}^{2}$=18,
甲数小于乙数的基本事件有:
(5,6),(5,7),(5,8),(5,9),(5,10),
∴甲数大于乙数的概率为p=1-$\frac{5}{18}$=$\frac{13}{18}$.
故答案为:$\frac{13}{18}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$cm | B. | $\frac{{π}^{2}}{3}$cm | C. | $\frac{2π}{3}$cm | D. | $\frac{2{π}^{2}}{3}$cm |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一个人打靶,打了10发子弹,有7发子弹中靶,因此这个人中靶的概率为0.7 | |
| B. | 一个同学做掷硬币试验,掷了6次,一定有3次“正面朝上” | |
| C. | 某地发行福利彩票,其回报率为47%,有个人花了100元钱买彩票,一定会有47元的回报 | |
| D. | 大量试验后,一个事件发生的频率在0.75附近波动,可以估计这个事件发生的概率为0.75 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:选择题
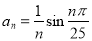 ,
,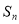 是
是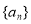 的前
的前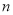 项和.在
项和.在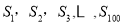 中,正数的个数是( )
中,正数的个数是( )
A.25 B.50 C.75 D.100
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,+∞) | C. | [3${\;}^{\frac{1}{1-ln2}}$,+∞) | D. | (2,3${\;}^{\frac{1}{1-ln2}}$] |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:解答题
面对某种流感病毒,各国医疗科研机构都在研究疫苗,现有A、B、C三个独立的研究机构在一定的时期研制出疫苗的概率分别为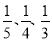 .求:
.求:
(1)他们能研制出疫苗的概率;
(2)至多有一个机构研制出疫苗的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com