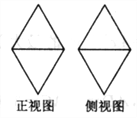
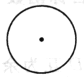
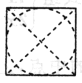
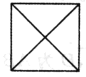
[题目]某几何体的正视图与侧视图如图所示.则它的俯视图不可能是( )A. B. C. D. 题目和参考答案——青夏教育精英家教网—

【题目】某几何体的正视图与侧视图如图所示，则它的俯视图不可能是（）

A. B. C. D.

【答案】C

【解析】若几何体为两个圆锥体的组合体,则俯视图为A;若几何体为四棱锥与圆锥的组合体,则俯视图为B;若几何体为两个四棱锥的组合体,则俯视图为D;不可能为C,故选C.

点睛: 思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如下图，在四棱锥中，面，，，，，，，为的中点。

（1）求证：面；

（2）线段上是否存在一点，满足？若存在，试求出二面角的余弦值；若不存在，说明理由。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某校从学生会宣传部6名成员(其中男生4人，女生2人)中，任选3人参加某省举办的“我看中国改革开放三十年”演讲比赛活动．

(1)设所选3人中女生人数为ξ，求ξ的分布列；

(2)求男生甲或女生乙被选中的概率；

(3)设“男生甲被选中”为事件A，“女生乙被选中”为事件B，求P(B)和P(B|A)．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知圆的圆心为原点，其半径与椭圆的左焦点和上顶点的连线线段长度相等.

（1）求圆的标准方程；

（2）过椭圆右焦点的动直线（其斜率不为0）交圆于两点，试探究在轴正半轴上是否存在定点，使得直线与的斜率之和为0？若存在，求出点的坐标，若不存在，请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】选修4-4：坐标系与参数方程

以平面直角坐标系的原点为极点，轴的正半轴为极轴，取相同的长度单位建立极坐标系，已知直线的极坐标方程是，圆的参数方程为（为参数，）.

（1）若直线与圆有公共点，求实数的取值范围；

（2）当时，过点且与直线平行的直线交圆于两点，求的值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在矩形中，，，点是线段上靠近点的一个三等分点，点是线段上的一个动点，且.如图，将沿折起至，使得平面平面.

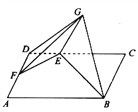
（1）当时，求证：；

（2）是否存在，使得与平面所成的角的正弦值为？若存在，求出的值；若不存在，请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势．某机构为了解某城市市民的年龄构成，按的比例从年龄在20～80岁(含20岁和80岁)之间的市民中随机抽取600人进行调查，并将年龄按进行分组，绘制成频率分布直方图，如图所示．规定年龄在岁的人为“青年人”，岁的人为“中年人”，岁的人为“老年人”．