
【题目】已知![]() 是正三棱柱,D是AC中点.
是正三棱柱,D是AC中点.
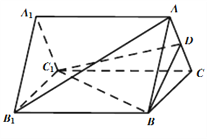
(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的度数.
的度数.
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
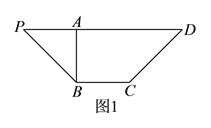
【题目】如图![]() ,等腰梯形
,等腰梯形![]() 中,
中, ![]() ,
, ![]() 于点
于点![]() ,
, ![]() ,且
,且![]() .沿
.沿![]() 把
把![]() 折起到
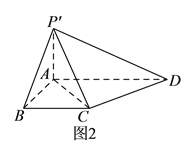
折起到![]() 的位置(如图
的位置(如图![]() ),使
),使![]() .
.
(I)求证: ![]() 平面
平面![]() .
.
(II)求三棱锥![]() 的体积.
的体积.
(III)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,指出点
,若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 4 | 19 | 20 | 5 | 1 |
图1:乙套设备的样本的频率分布直方图

(1)填写下面列联表,并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关;
甲套设备 | 乙套设备 | 合计 | |||||||||||||
合格品 | |||||||||||||||
不合格品 | |||||||||||||||
合计 | ,求 |
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明设置的手机开机密码若连续3次输入错误,则手机被锁定,5分钟后,方可重新输入.
某日,小明忘记了开机密码,但可以确定正确的密码是他常用的4个密码之一,于是,他
决定逐个(不重复)进行尝试.
(1)求手机被锁定的概率;
(2)设第![]() 次输入后能成功开机,求
次输入后能成功开机,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上的动点,点
是圆上的动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]() ,
, ![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,直线
相切,直线![]() 与(1)中所求点
与(1)中所求点![]() 的轨迹交于不同的两点
的轨迹交于不同的两点![]() ,
, ![]() ,
, ![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ex-![]() (x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
A. (-∞,![]() ) B. (-∞,
) B. (-∞,![]() )
)
C. (-![]() ,
, ![]() ) D. (-
) D. (-![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥S-ABCD中,SA=AB=2,E,F,G分别为BC,SC,CD的中点.设P为线段FG上任意一点.
(1)求证:EP⊥AC;
(2)当P为线段FG的中点时,求直线BP与平面EFG所成角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A. 导函数为![]()
B. 函数f(x)的图象关于直线![]() 对称
对称
C. 函数f(x)在区间![]() 上是增函数
上是增函数
D. 函数f(x)的图象可由函数y=3cos 2x的图象向右平移![]() 个单位长度得到
个单位长度得到
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com