
分析 (1)根据f(x)-2=0的两根分别为-3和1,可设f(x)-2=a(x+3)(x-1),将(0,-1)代入整理可得f(x)的解析式.
(2)在区间[0,2]上,y=f(x)的图象恒在直线y=kx-3的上方,即k<x+$\frac{2}{x}$+2恒成立,结合对勾函数的图象和性质,可得k的范围.
解答 解:(1)∵f(x)-2=0的两根分别为-3和1,
∴f(x)-2=a(x+3)(x-1),
又由f(0)=-1,
∴a=1,
∴f(x)-2=(x+3)(x-1),
即f(x)=x2+2x-1,
(2)若在区间[0,2]上,y=f(x)的图象恒在直线y=kx-3的上方,
则在区间[0,2]上,x2+2x-1>kx-3恒成立,
当x=0时,不等式显然成立,
当x∈(0,2]时,k<x+$\frac{2}{x}$+2恒成立,
令g(x)=x+$\frac{2}{x}$+2,由对勾函数图象和性质,可得当x=$\sqrt{2}$时,函数g(x)取最小值2+2$\sqrt{2}$,
故k<2+2$\sqrt{2}$.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
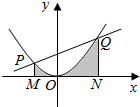
| A. | $\frac{65}{12}$ | B. | $\frac{85}{16}$ | C. | $\frac{143}{24}$ | D. | $\frac{95}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 学校组织“踢毽球”大赛,某班为了选出一人参加比赛,对班上甲乙两位同学进行了8次测试,且每次测试之间是相互独立.成绩如下:(单位:个/分钟)
学校组织“踢毽球”大赛,某班为了选出一人参加比赛,对班上甲乙两位同学进行了8次测试,且每次测试之间是相互独立.成绩如下:(单位:个/分钟)| 甲 | 80 | 81 | 93 | 72 | 88 | 75 | 83 | 84 |
| 乙 | 82 | 93 | 70 | 84 | 77 | 87 | 78 | 85 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
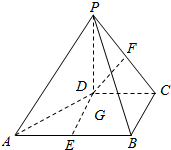 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=CB=1,BA=2,AB∥DC,∠BCD=90°,点E、F、G分别是线段AB、PC、DE的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=CB=1,BA=2,AB∥DC,∠BCD=90°,点E、F、G分别是线段AB、PC、DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[2-\sqrt{2},2+\sqrt{2}]$ | B. | $(2-\sqrt{2},2+\sqrt{2})$ | C. | [1,3] | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com