
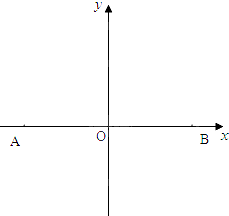
 如图,A,B两地相距10km,A(-5,0),B(5,0).有一种商品,A、B两地均有出售且价格相同,某地居民从两地之一购得商品运回来,每公里的运费A地是B地的3倍.问该地居民应如何选择A地或B地购买此种商品最合算?(仅从运费的多少来考虑)
如图,A,B两地相距10km,A(-5,0),B(5,0).有一种商品,A、B两地均有出售且价格相同,某地居民从两地之一购得商品运回来,每公里的运费A地是B地的3倍.问该地居民应如何选择A地或B地购买此种商品最合算?(仅从运费的多少来考虑)| (x+5)2+y2 |
| (x-5)2+y2 |
| 25 |
| 4 |
| 15 |
| 4 |
| 25 |
| 4 |
| 15 |
| 4 |


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
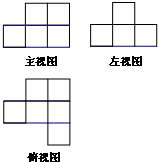 在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要清点一下箱子的数量,于是就想出一个办法:将这堆货物的三视图画了出来,你能根据三视图,帮他清点一下箱子的数量吗?这些正方体货箱的个数为( )
在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要清点一下箱子的数量,于是就想出一个办法:将这堆货物的三视图画了出来,你能根据三视图,帮他清点一下箱子的数量吗?这些正方体货箱的个数为( )| A、6 | B、7 | C、8 | D、9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
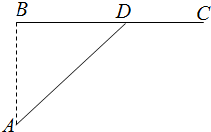 如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com