
【题目】如图,已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点, ![]() ,
, ![]() .
.
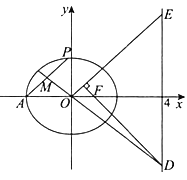
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为原点,
为原点, ![]() 为椭圆上一点,
为椭圆上一点, ![]() 的中点为
的中点为![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,过
,过![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(1)由题中条件要得两个等式,再由椭圆中![]() 的等式关系可得
的等式关系可得![]() 的值,求得椭圆的方程;
的值,求得椭圆的方程;
(2)可设直线![]() 的方程,联立椭圆方程,由根与系数的关系得
的方程,联立椭圆方程,由根与系数的关系得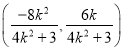 ,所以直线
,所以直线![]() 的方程是
的方程是 ![]() .令
.令![]() ,得
,得![]() , 得直线
, 得直线![]() 的斜率是
的斜率是 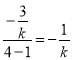 ,问题得解.
,问题得解.
试题解析:

(Ⅰ)设椭圆![]() 的半焦距为
的半焦距为![]() .依题意,得
.依题意,得![]() ,
, ![]() .
.
解得 ![]() ,
, ![]() .所以
.所以 ![]() ,所以椭圆
,所以椭圆![]() 的方程是
的方程是 ![]() .
.
(Ⅱ)解法一:由(Ⅰ)得 ![]() .设
.设![]() 的中点
的中点![]() ,
, ![]() .
.
设直线![]() 的方程为:
的方程为: ![]() ,将其代入椭圆方程,整理得
,将其代入椭圆方程,整理得
![]() ,所以
,所以 ![]() .所以
.所以 ![]() ,
, ![]() ,
,
即 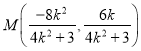 .所以直线
.所以直线![]() 的斜率是
的斜率是  ,
,
所以直线![]() 的方程是
的方程是 ![]() .令
.令![]() ,得
,得![]() .
.
由![]() ,得直线
,得直线![]() 的斜率是
的斜率是 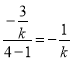 ,
,
因为![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() .
.
解法二:由(Ⅰ)得 ![]() .设
.设![]() ,其中
,其中![]() .
.
因为![]() 的中点为
的中点为![]() ,所以
,所以 ![]() .所以直线
.所以直线![]() 的斜率是
的斜率是 ![]() ,所以直线
,所以直线![]() 的方程是
的方程是 ![]() .令
.令![]() ,得
,得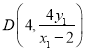 .
.
由![]() ,得直线
,得直线![]() 的斜率是
的斜率是 ![]() .因为直线
.因为直线![]() 的斜率是
的斜率是 ![]() ,所以
,所以 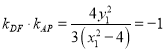 ,所以
,所以 ![]() .因为
.因为 ![]() ,所以
,所以 ![]() .
.
点晴:本题主要考查直线与圆锥曲线位置关系. 直线和圆锥曲线的位置关系一方面要体现方程思想,另一方面要结合已知条件,从图形角度求解.联立直线与圆锥曲线的方程得到方程组,化为一元二次方程后由根与系数的关系求解是一个常用的方法. 涉及弦长的问题中,应熟练地利用根与系数关系、设而不求法计算弦长;涉及垂直关系时也往往利用根与系数关系、设而不求法简化运算;涉及过焦点的弦的问题,可考虑用圆锥曲线的定义求解.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】某港口有一个泊位,现统计了某月100艘轮船在该泊位停靠的时间(单位:小时),如果停靠时间不足半小时按半小时计时,超过半小时不足1小时按1小时计时,以此类推,统计结果如表:
停靠时间 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
轮船数量 | 12 | 12 | 17 | 20 | 15 | 13 | 8 | 3 |
(Ⅰ)设该月100艘轮船在该泊位的平均停靠时间为![]() 小时,求
小时,求![]() 的值;
的值;
(Ⅱ)假定某天只有甲、乙两艘轮船需要在该泊位停靠![]() 小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年时红军长征胜利80周年,某市电视台举办纪念红军长征胜利80周年知识问答,宣传长征精神.首先在甲、乙、丙、丁四个不同的公园进行支持签名活动,其次在各公园签名的人中按分层抽样的方式抽取10名幸运之星,每人获得一个纪念品,其数据表格如下:

(Ⅰ)求此活动中各公园幸运之星的人数;
(Ⅱ)从乙和丙公园的幸运之星中任选两人接受电视台记者的采访,求这两人均来自乙公园的概率;
(Ⅲ)电视台记者对乙公园的签名人进行了是否有兴趣研究“红军长征”历史的问卷调查,统计结果如下(单位:人):

据此判断能否在犯错误的概率不超过0.01的前提下认为有兴趣研究“红军长征”历史与性别有关.
附临界值表及公式:  ,其中
,其中![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点, ![]() ,
, ![]() .
.
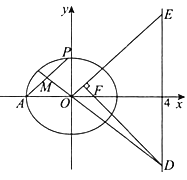
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为原点,
为原点, ![]() 为椭圆上一点,
为椭圆上一点, ![]() 的中点为
的中点为![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,过
,过![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,以上顶点和右焦点为直径端点的圆与直线
,以上顶点和右焦点为直径端点的圆与直线![]() 相切.
相切.
(1)求椭圆的标准方程;
(2)对于直线![]() 和点
和点![]() ,椭圆
,椭圆![]() 上是否存在不同的两点
上是否存在不同的两点![]() 与
与![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,若存在实数
,若存在实数![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)设曲线![]() 在
在![]() 处的切线为
处的切线为![]() ,若
,若![]() 与点
与点![]() 的距离为
的距离为![]() ,求
,求![]() 的值;
的值;
(2)若对于任意实数![]() ,
, ![]() 恒成立,试确定
恒成立,试确定![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com