
【题目】已知椭圆C:![]() 的焦距为2,左右焦点分别为
的焦距为2,左右焦点分别为![]() ,
,![]() ,以原点O为圆心,以椭圆C的半短轴长为半径的圆与直线
,以原点O为圆心,以椭圆C的半短轴长为半径的圆与直线![]() 相切.
相切.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 设不过原点的直线l:
设不过原点的直线l:![]() 与椭圆C交于A,B两点.
与椭圆C交于A,B两点.
![]() 若直线
若直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,求证:直线l过定点,并求出该定点的坐标;
,求证:直线l过定点,并求出该定点的坐标;
![]() 若直线l的斜率是直线OA,OB斜率的等比中项,求
若直线l的斜率是直线OA,OB斜率的等比中项,求![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() ;(2)(i)直线
;(2)(i)直线![]() 过定点,该定点的坐标为
过定点,该定点的坐标为![]() ;(ii)
;(ii)![]() 面积的取值范围为
面积的取值范围为![]()
【解析】
试题(1)先根据抛物线![]() 的焦点
的焦点![]() 得
得![]() ,再结合椭圆几何条件得当点
,再结合椭圆几何条件得当点![]() 为椭圆的短轴端点时,△
为椭圆的短轴端点时,△![]() 面积最大,此时
面积最大,此时![]() ,所以
,所以![]() .(2)(i)证明直线过定点问题,一般方法以算代证,即求出直线方程,根据方程特征确定其过定点,本题关键求出
.(2)(i)证明直线过定点问题,一般方法以算代证,即求出直线方程,根据方程特征确定其过定点,本题关键求出![]() 之间关系即可得出直线过定点.由
之间关系即可得出直线过定点.由![]() 得
得![]() ,即
,即![]() ,因此联立直线与椭圆方程,结合韦达定理可得;(ii)先分析条件:直线
,因此联立直线与椭圆方程,结合韦达定理可得;(ii)先分析条件:直线![]() 的斜率时直线
的斜率时直线![]() ,
,![]() 斜率的等比中项,即
斜率的等比中项,即![]() ,
,![]() ,化简得
,化简得![]() ,联立直线与椭圆方程,结合韦达定理可得
,联立直线与椭圆方程,结合韦达定理可得![]() ,这样三角形面积可用m表示,其中高利用点到直线距离得到,底边边长利用弦长公式得到:
,这样三角形面积可用m表示,其中高利用点到直线距离得到,底边边长利用弦长公式得到:![]() ,最后根据基本不等式求最值
,最后根据基本不等式求最值
试题解析:(1)由抛物线的方程![]() 得其焦点为
得其焦点为![]() ,所以椭圆中
,所以椭圆中![]() ,
,
当点![]() 为椭圆的短轴端点时,△
为椭圆的短轴端点时,△![]() 面积最大,此时
面积最大,此时![]() ,所以
,所以![]() .
.
![]() ,
,![]() 为椭圆的左、右焦点,
为椭圆的左、右焦点,![]() 为椭圆上任意一点,△
为椭圆上任意一点,△![]() 面积的最大值为1,
面积的最大值为1,
所以椭圆的方程为![]() .
.
(2)联立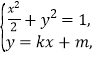 得
得![]() ,
,
![]() ,得
,得![]() (*)
(*)
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
(i)![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,
,
所以![]() ,即
,即![]() ,
,
得![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,因此直线
,因此直线![]() 恒过定点,该定点坐标为
恒过定点,该定点坐标为![]() .
.
(ii)因为直线![]() 的斜率是直线
的斜率是直线![]() ,
,![]() 斜率的等比中项,所以
斜率的等比中项,所以![]() ,即
,即![]() ,
,
得![]() ,得
,得![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
代入(*),得![]() .
.
![]() .
.
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]() ,
,
所以![]()
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时,△
时,△![]() 面积取最大值
面积取最大值![]() .
.
故△![]() 面积的取值范围为
面积的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】(本小题共14分)如图,在三棱锥![]() 中,
中, ![]() 底面
底面
![]() ,点
,点![]() ,
, ![]() 分别在棱
分别在棱![]() 上,且
上,且![]() (Ⅰ)求证:
(Ⅰ)求证: ![]() 平面
平面![]() ;(Ⅱ)当
;(Ⅱ)当![]() 为
为![]() 的中点时,求
的中点时,求![]() 与平面
与平面![]() 所成的角的大小;(Ⅲ)是否存在点
所成的角的大小;(Ⅲ)是否存在点![]() 使得二面角
使得二面角![]() 为直二面角?并说明理由.
为直二面角?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两圆![]() 的圆心分别为
的圆心分别为![]() ,P为一个动点,且直线
,P为一个动点,且直线![]() 的斜率之积为
的斜率之积为![]() .
.
(Ⅰ)求动点P的轨迹M的方程;
(Ⅱ)是否存在过点A(2,0)的直线l与轨迹M交于不同的两点C、D,使得![]() ?若存在,求直线l的方程;若不存在,请说明理由.
?若存在,求直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为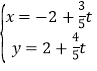 (t为参数),它与曲线
(t为参数),它与曲线
C:(y-2)2-x2=1交于A、B两点.
(1)求|AB|的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为![]() ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,某企业每年消耗电费约24万元,为了节能减排,决定安装一个可使用15年的太阳能供电设备接入本企业电网,安装这种供电设备的工本费(单位:万元)与太阳能电池板的面积(单位:平方米)成正比,比例系数约为0.5.为了保证正常用电,安装后采用太阳能和电能互补供电的模式.假设在此模式下,安装后该企业每年消耗的电费![]() (单位:万元)与安装的这种太阳能电池板的面积
(单位:万元)与安装的这种太阳能电池板的面积![]() (单位:平方米)之间的函数关系是
(单位:平方米)之间的函数关系是![]() 为常数).记
为常数).记![]() 为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
(1)试解释![]() 的实际意义,并建立
的实际意义,并建立![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为多少平方米时,
为多少平方米时,![]() 取得最小值?最小值是多少万元?
取得最小值?最小值是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求证:函数f(x)-g(x)必有零点;
(2)设函数G(x)=f(x)-g(x)-1
①若函数G(x)有两相异零点且![]() 在
在![]() 上是减函数,求实数m的取值范围。
上是减函数,求实数m的取值范围。
②是否存在整数a,b使得![]() 的解集恰好为
的解集恰好为![]() 若存在,求出a,b的值,若不存在,请说明理由。
若存在,求出a,b的值,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但蔬菜上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水![]() (单位:千克)清洗蔬菜
(单位:千克)清洗蔬菜![]() 千克后,蔬菜上残留的农药
千克后,蔬菜上残留的农药![]() (单位:微克)的统计表:
(单位:微克)的统计表:
|
|
|
|
|
|
|
|
|
|
|
|
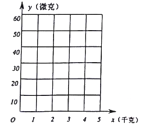
(1)在下面的坐标系中,描出散点图,并判断变量![]() 与
与![]() 是正相关还是负相关;
是正相关还是负相关;
(2)若用解析式![]() 作为蔬菜农药残量
作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程,令
的回归方程,令![]() ,计算平均值
,计算平均值![]() 与
与![]() ,完成以下表格(填在答题卡中),求出
,完成以下表格(填在答题卡中),求出![]() 与
与![]() 的回归方程.(
的回归方程.(![]() 保留两位有效数字);
保留两位有效数字);
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
(3)对于某种残留在蔬菜上的农药,当它的残留量低于![]() 微克时对人体无害,为了放心食用该蔬菜,请评估需要用多少千克的清水清洗一千克蔬菜?(精确到
微克时对人体无害,为了放心食用该蔬菜,请评估需要用多少千克的清水清洗一千克蔬菜?(精确到![]() ,参考数据
,参考数据![]() )(附:对于一组数据
)(附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: 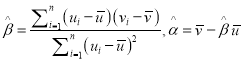 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com