
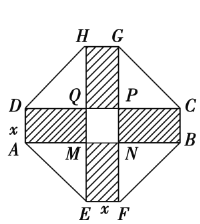
【题目】某居民小区要建造一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的,是面积为200平方米的十字形地带.计划在正方MNPQ上建一座花坛,造价是每平方米4 200元,在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价是每平方米210元,再在四个空角上铺上草坪,造价是每平方米80元.
(1)设总造价是S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出最小值.
科目:高中数学 来源: 题型:
【题目】【2017届陕西省西安市铁一中学高三上学期第五次模拟考试数学(文)】已知向量![]() ,
,![]() ,且函数
,且函数![]() .
.
(Ⅰ)当函数在![]() 上的最大值为3时,求
上的最大值为3时,求的值;
(Ⅱ)在(Ⅰ)的条件下,若对任意的![]() ,函数
,函数,![]() 的图像与直线
的图像与直线有且仅有两个不同的交点,试确定的值.并求函数在上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“开门大吉”是中央电视台推出的娱乐节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌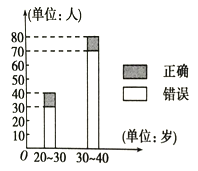
的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
(1) 完成下列2×2列联表(见答题纸);
(2)判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由.(下面的临界值表供参考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(参考公式: 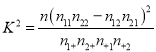 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式:
(1)![]() ;
;
(2)已知![]() ,则
,则![]() ;
;
(3)函数![]() 的图象与函数
的图象与函数![]() 的图象关于y轴对称;
的图象关于y轴对称;
(4)函数![]() 的定义域是R,则m的取值范围是
的定义域是R,则m的取值范围是![]() ;
;
(5)函数![]() 的递增区间为
的递增区间为![]() .
.
正确的有______________________.(把你认为正确的序号全部写上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到下图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).
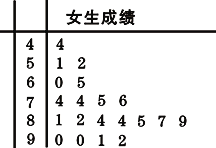
(1)请根据题意,将2×2列联表补充完整;
优秀 | 非优秀 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(2)据此列联表判断,是否有90%的把握认为该学科成绩与性别有关?
附: 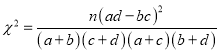 ,其中
,其中![]() .
.
参考数据 | 当 |
当 | |
当 | |
当 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税法》规定,公民全月工资所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额,此项税款按下表分段累计计算:

(1)某人10月份应交此项税款为350元,则他10月份的工资收入是多少?
(2)假设某人的月收入为![]() 元,
元, ![]() ,记他应纳税为
,记他应纳税为![]() 元,求
元,求![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有两个课外活动小组,其中第一小组有足球票6张,排球票4张;第二个小组有
足球票4张,排球票6张.甲从第一小组的10张票中任抽1张,乙从第二小组的10
张票中任抽1张.
(1)两人都抽到足球票的概率是多少?
(2)两人中至少有一人抽到足球票的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com