
【题目】已知函数![]() ,
,![]() .
.
(1)记![]() ,试判断函数
,试判断函数![]() 的极值点的情况;
的极值点的情况;
(2)若![]() 有且仅有两个整数解,求
有且仅有两个整数解,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对GDP增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合图,下列说法不正确的是( )
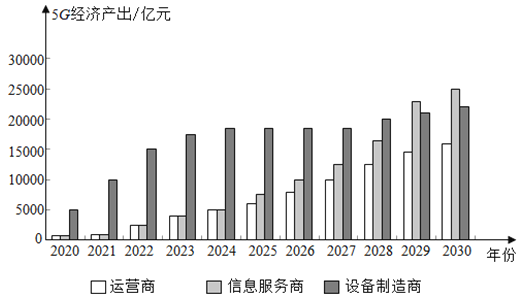
A.5G的发展带动今后几年的总经济产出逐年增加
B.设备制造商的经济产出前期增长较快,后期放缓
C.设备制造商在各年的总经济产出中一直处于领先地位
D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.
是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.
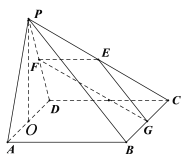
(Ⅰ)求证:PO平面![]() ;
;
(Ⅱ)求平面EFG与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,若存在,求线段
,若存在,求线段![]() 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期. 一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
(1)求这1000名患者的潜伏期的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表. 请将列联表补充完整,并根据列联表判断是否有![]() 的把握认为潜伏期与患者年龄有关;
的把握认为潜伏期与患者年龄有关;
潜伏期 | 潜伏期 | 总计 | |
50岁以上(含50岁) |
| ||
50岁以下 | 55 | ||
总计 | 200 |
(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立. 为了深入研究,该研究团队随机调查了![]() 名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:
|
|
| |
|
|
|
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且过点
,且过点![]() .
.
(1)求椭圆的方程;
(2)已知![]() ,是否存在k使得点A关于l的对称点B(不同于点A)在椭圆C上?若存在求出此时直线l的方程,若不存在说明理由.
,是否存在k使得点A关于l的对称点B(不同于点A)在椭圆C上?若存在求出此时直线l的方程,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九世纪末,法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”,即“在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少?”贝特朗用“随机半径”、“随机端点”、“随机中点”三个合理的求解方法,但结果都不相同.该悖论的矛头直击概率概念本身,强烈地刺激了概率论基础的严格化.已知“随机端点”的方法如下:设A为圆O上一个定点,在圆周上随机取一点B,连接AB,所得弦长AB大于圆O的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com