
【题目】已知函数f(x)=x2﹣ax+b(a>0,b>0)有两个不同的零点m,n,且m,n和﹣2三个数适当排序后,即可成为等差数列,也可成为等比数列,则a+b的值为( )
A.7
B.8
C.9
D.10
科目:高中数学 来源: 题型:
【题目】电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧播放时长(分钟) | 广告播放时长(分钟) | 收视人次(万) | |
甲 | 70 | 5 | 60 |
乙 | 60 | 5 | 25 |
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x,y表示每周计划播出的甲、乙两套连续剧的次数.(13分)
(I)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域;
(II)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD-A1B1C1D1中,AB=3,AD=2,AA1=1,以长方体的八个顶点中的两点为起点和终点的向量中.

(1)单位向量共有多少个?
(2)试写出模为![]() 的所有向量.
的所有向量.
(3)试写出与![]() 相等的所有向量.
相等的所有向量.
(4)试写出![]() 的相反向量.
的相反向量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两工人在同样的条件下生产,日产量相等,每天出废品的情况如下表:

则下列结论中正确的是 ( )
A. 甲生产的产品质量比乙生产的产品质量好一些
B. 乙生产的产品质量比甲生产的产品质量好一些
C. 两人生产的产品质量一样好
D. 无法判断谁生产的产品质量好一些
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的生产部门调研发现,该公司第二、三季度的月用电量与月份线性相关,且数据统计如下表:

但核对电费报表时发现一组数据统计有误.
(1)请指出哪组数据有误,并说明理由;
(2)在排除有误数据后,求月用电量与月份之间的回归方程,并预测统计有误月份的用电量.(结果精确到0.1)
附注: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平行四边形ABCD中,∠A=45°,且AB=BD=1,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图所示:
(1)求证:AB⊥CD;
(2)若M为AD的中点,求二面角A﹣BM﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且a,b,c成等比数列,sinB= ![]() ,
,
(1)求 ![]() +
+ ![]() 的值;
的值;
(2)若 ![]()
![]() =12,求a+c的值.
=12,求a+c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知CD是等边三角形ABC的AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
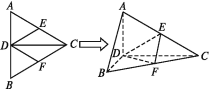
(1)求直线BC与平面DEF所成角的余弦值;
(2)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com