
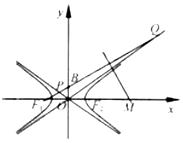
 如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M,若|MF2|=|F1F2|,则双曲线C的渐近线方程是( )
如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M,若|MF2|=|F1F2|,则双曲线C的渐近线方程是( )| A. | y=±x | B. | $y=±\sqrt{3}x$ | C. | $y=±\frac{1}{2}x$ | D. | $y=±\frac{{\sqrt{2}}}{2}x$ |
分析 由题意知直线F1B的方程为y=$\frac{b}{c}x+b$,分别与双曲线的渐近线联立,得到P,Q的坐标,从而得到PQ的中点坐标,进而求出PQ的垂直平分线方程,推导出a与b的等量关系,由此能求出双曲线C的渐近线方程.
解答 解:由题意知直线F1B的方程为y=$\frac{b}{c}x+b$,
联立$\left\{\begin{array}{l}{y=\frac{b}{c}x+b}\\{\frac{{x}^{\;}}{{a}^{\;}}-\frac{{y}^{\;}}{{b}^{\;}}=0}\end{array}\right.$,得Q($\frac{ac}{c-a},\frac{bc}{c-a}$),
联立$\left\{\begin{array}{l}{y=\frac{b}{a}x+b}\\{\frac{x}{a}+\frac{y}{b}=0}\end{array}\right.$,得P(-$\frac{ac}{c+a},\frac{bc}{c+a}$),
∴PQ的中点为($\frac{{a}^{2}c}{{b}^{2}}$,$\frac{{c}^{2}}{{b}^{2}}$),
∴PQ的垂直平分线方程为y-$\frac{{c}^{2}}{b}$=-$\frac{c}{b}$(x-$\frac{{a}^{2}c}{{b}^{2}}$),
令y=0,得x=c(1+$\frac{{a}^{2}}{{b}^{2}}$),∴(1+$\frac{{a}^{2}}{{b}^{2}}$)=3c,
∴a2=2b2,
∴双曲线C的渐近线方程y=$±\frac{\sqrt{2}}{2}$x.
故选:D.
点评 本题考查双曲线的渐近线方程的求法,是中档题,解题时要认真审题,注意双曲线性质的合理运用.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{e}$] | B. | (-∞,e] | C. | $({\frac{1}{e},+∞})$ | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{4})$ | B. | $(\frac{1}{3},3)$ | C. | (1,2) | D. | $(2,\frac{9}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
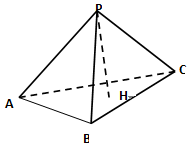 已知P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面 ABC,H,则H为△ABC的( )
已知P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面 ABC,H,则H为△ABC的( )| A. | 重心 | B. | 垂心 | C. | 外心 | D. | 内心 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com