
【题目】已知函数![]() 上的一个最高点的坐标为
上的一个最高点的坐标为![]() ,由此点到相邻最低点间的曲线与x轴交于点
,由此点到相邻最低点间的曲线与x轴交于点![]() ,若
,若![]() .
.
(1)求![]() 的解析式.
的解析式.
(2)求![]() 在
在![]() 上的值域.
上的值域.
(3)若对任意实数![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
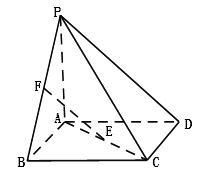
【题目】如图,四棱锥 ![]() 的底面
的底面 ![]() 为正方形,
为正方形, ![]() ⊥底面
⊥底面 ![]() ,
, ![]() 分别是
分别是 ![]() 的中点,
的中点, ![]() .
.
(Ⅰ)求证 ![]() ∥平面
∥平面 ![]() ;
;
(Ⅱ)求直线 ![]() 与平面
与平面 ![]() 所成的角;
所成的角;
(Ⅲ)求四棱锥 ![]() 的外接球的体积.
的外接球的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 的部分图象如图所示.
的部分图象如图所示.
(1)求函数![]() 的解析式;
的解析式;
(2)将![]() 的图象向左平移
的图象向左平移![]() 个单位长度得到
个单位长度得到![]() 的图象,若
的图象,若![]() 图象的一个对称轴为
图象的一个对称轴为![]() ,求
,求![]() 的最小值;
的最小值;
(3)在第(2)问的前提下,求函数![]() 在
在![]() 上的单调区间.
上的单调区间.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|ax﹣1|.
(Ⅰ)若f(x)≤2的解集为[﹣6,2],求实数a的值;
(Ⅱ)当a=2时,若存在x∈R,使得不等式f(2x+1)﹣f(x﹣1)≤7﹣3m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在著名的汉诺塔问题中有三根针和套在一根针上的若干金属片,按下列规则,把金属片从一根针上全部移到另一根针上:①每次只能移动一个金属片;②在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.将n个金属片从1号针移到3号针最少需要移动的次数记为f(n),则f(6)=( ) 
A.31
B.33
C.63
D.65
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足a1=2,b1=4,且 2bn=an+an+1 , an+12=bnbn+1 .
(Ⅰ)求 a 2 , a3 , a4 及b2 , b3 , b4;
(Ⅱ)猜想{an},{bn} 的通项公式,并证明你的结论;
(Ⅲ)证明:对所有的 n∈N* , ![]()
![]() …
… ![]() <
< ![]() <
< ![]() sin
sin ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE. 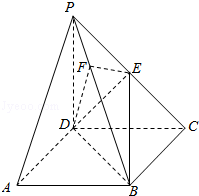
(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(2)若面DEF与面ABCD所成二面角的大小为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥P﹣ABCD中,∠ABC=60°,PA=AC=a,PB=PD= ![]() ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.
(Ⅰ)证明PA⊥平面ABCD;
(Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的大小;
(Ⅲ)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com