
【题目】已知动点![]() 在
在![]() 轴上方,且到定点
轴上方,且到定点![]() 距离比到
距离比到![]() 轴的距离大
轴的距离大![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() ,
,![]() 分别异于原点
分别异于原点![]() ,在曲线
,在曲线![]() 的
的![]() ,
,![]() 两点处的切线分别为
两点处的切线分别为![]() ,
,![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证:![]() 在定直线上.
在定直线上.
科目:高中数学 来源: 题型:
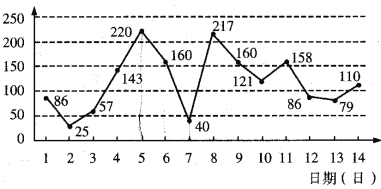
【题目】下图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表.某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
空气质量指数 | 污染程度 |
小于100 | 优良 |
大于100且小于150 | 轻度 |
大于150且小于200 | 中度 |
大于200且小于300 | 重度 |
(1)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(2)求此人到达当日空气质量优良的概率;
(3)求此人出差期间(两天)空气质量至少有一天为中度或重度污染的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月25日-27日,北京召开第二届“一带一路”国际高峰论坛,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角BCGA的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有9只球,其中标有数字1,2,3,4的小球各2个,标数字5的小球有1个.从袋中任取3个小球,每个小球被取出的可能性都相等,用![]() 表示取出的3个小球上的最大数字.
表示取出的3个小球上的最大数字.
(1)求取出的3个小球上的数字互不相同的概率;
(2)求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为定义域R上的奇函数,且在R上是单调递增函数,函数
为定义域R上的奇函数,且在R上是单调递增函数,函数![]() ,数列
,数列![]() 为等差数列,且公差不为0,若
为等差数列,且公差不为0,若![]() ,则
,则![]() ( )
( )
A. 45B. 15C. 10D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com