
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L⊥直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。试建立适当的直角坐标系,解决下列问题: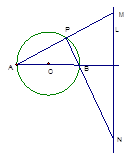
(1)若∠PAB=30°,求以MN为直径的圆方程;
(2)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
(1)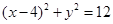 ;(2)详见答案。
;(2)详见答案。
解析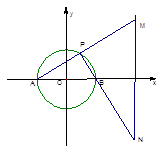
试题分析:(1)建立如图所示的直角坐标系,⊙O的方程为 ,直线L的方程为
,直线L的方程为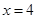 。……2分
。……2分
(1)∵∠PAB=30°,∴点P的坐标为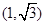 ,
,
∴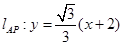 ,
,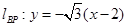 。将x=4代入,
。将x=4代入,
得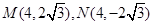 ……4分
……4分
。∴MN的中点坐标为(4,0),MN=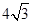 。 ……6分
。 ……6分
∴以MN为直径的圆的方程为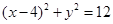 。同理,当点P在x轴下方时,所求圆的方程仍是
。同理,当点P在x轴下方时,所求圆的方程仍是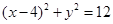 。 ……8分
。 ……8分
(2)设点P的坐标为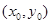 ,∴
,∴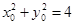 (
(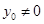 ),∴
),∴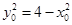 。
。
∵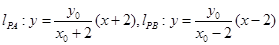 ,将x=4代入,得
,将x=4代入,得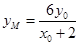 ,
,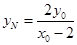 。 ……10分
。 ……10分
∴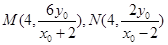 ,MN=
,MN= 。MN的中点坐标为
。MN的中点坐标为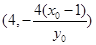 。 ……12分
。 ……12分
以MN为直径的圆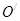 截x轴的线段长度为
截x轴的线段长度为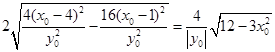
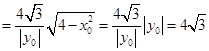 为定值。
为定值。
∴⊙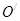 必过⊙O 内定点
必过⊙O 内定点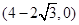 。 ……16分
。 ……16分
考点:本题考查了用解析法求圆的方程及性质。
点评:用待定系数法求圆的方程要注意两点:第一,究竟用标准方程还是一般方程要根据题设条件选择,选择得当,解法就简捷,选择不当,会增加解答的难度;第二,要注意适时运用几何知识列方程,这样可能大大减少运算量.


科目:高中数学 来源: 题型:
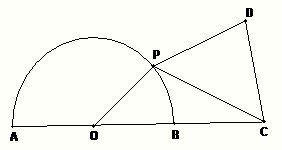 如图:已知圆O的直径是2,点C在直径AB的延长线上,BC=1,点P是圆O上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC的两侧,求四边形OPDC面积的最大值.
如图:已知圆O的直径是2,点C在直径AB的延长线上,BC=1,点P是圆O上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC的两侧,求四边形OPDC面积的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB.点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点.
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB.点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且AD=
如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且AD=| 1 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
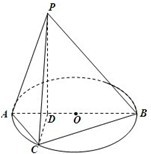 (2013•佛山一模)如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且AD=
(2013•佛山一模)如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且AD=| 1 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北衡水中学高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
(本题12分)
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。

(Ⅰ)若∠PAB=30°,求以MN为直径的圆方程;
(Ⅱ)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com