练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

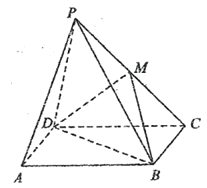
    【题目】如图，在四棱锥P—ABCD中，四边形ABCD是矩形，平面PCD⊥平面ABCD，M为PC中点．求证：

    （1）PA∥平面MDB；

    （2）PD⊥BC．

    【答案】（1）详见解析；（2）详见解析.

    【解析】

    试题分析：（1）线面平行的判定关键在证相应线线平行，线线平行的证明或寻求需要结合平面几何的知识，如中位线平行于底面，因为本题中M为PC中点，所以应取BD的中点作为解题突破口；（2）线线垂直的证明一般需要经过多次线线垂直与线面垂直的转化，而对于面面垂直，基本是单向转化，即作为条件，就将其转化为线面垂直；作为结论，只需寻求线面垂直.如本题中面PCD与面ABCD垂直，就转化为BC平面PCD，到此所求问题转化为:已知线面垂直，要求证线线垂直.在线线垂直与线面垂直的转化过程中，要注意充分应用平面几何中的垂直条件,如矩形邻边相互垂直.

    试题解析：证明：（1）连结AC交BD于点O,连结OM. 2分

    因为M为PC中点,O为AC中点，

    所以MO//PA. 4分

    因为MO平面MDB，PA平面MDB,

    所以PA//平面MDB. 7分

    （2）因为平面PCD平面ABCD,

    平面PCD平面ABCD =CD,

    BC平面ABCD ,BCCD,

    所以BC平面PCD. 12分

    因为PD平面PCD,

    所以BCPD 14分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知经销某种商品的电商在任何一个销售季度内，每售出吨该商品可获利润万元，未售出的商品，每吨亏损万元．根据往年的销售经验，得到一个销售季度内市场需求量的频率分布直方图如右图所示．已知电商为下一个销售季度筹备了吨该商品．现以（单位：吨， ）表示下一个销售季度的市场需求量， （单位：万元）表示该电商下一个销售季度内经销该商品获得的利润．

    （Ⅰ）根据频率分布直方图，估计一个销售季度内市场需求量的平均数与中位数的大小；

    （Ⅱ）根据直方图估计利润不少于57万元的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】交通指数是指交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念性指数值，记交通指数为，其范围为，分别有五个级别：，畅通；，基本畅通；，轻度拥堵；，中度拥堵；，严重拥堵.在晚高峰时段（），从某市交通指挥中心选取了市区20个交通路段，依据其交通指数数据绘制的频率分布直方图如图所示.

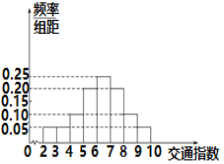
    (1)求出轻度拥堵、中度拥堵、严重拥堵的路段的个数；

    (2)用分层抽样的方法从轻度拥堵、中度拥堵、严重拥堵的路段中共抽取6个路段，求依次抽取的三个级别路段的个数；

    (3)从(2)中抽取的6个路段中任取2个，求至少有1个路段为轻度拥堵的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业为确定下一年投入某种产品的研发费用，需了解年研发费用（单位：千万元）对年销售量（单位：千万件）的影响，统计了近年投入的年研发费用与年销售量的数据，得到散点图如图所示．

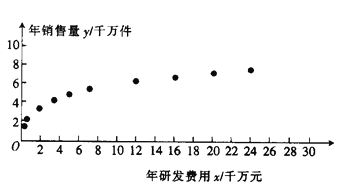
    (1)利用散点图判断和（其中均为大于的常数）哪一个更适合作为年销售量和年研发费用的回归方程类型（只要给出判断即可，不必说明理由）

    (2)对数据作出如下处理，令，得到相关统计量的值如下表：根据第(1)问的判断结果及表中数据，求关于的回归方程；

    15

    15

    28.25

    56.5

    (3)已知企业年利润（单位：千万元）与的关系为（其中），根据第(2)问的结果判断，要使得该企业下一年的年利润最大，预计下一年应投入多少研发费用?

    附：对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为，

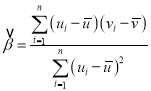    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）

    如图在直三棱柱ABC—A1B1C1中，AC=3，BC=4，AB=5，AA1=4,点D是AB的

    中点.

    (1) 求证： AC⊥BC1

    (2) 求证：AC1∥平面CDB1

    (3) 求异面直线AC1与B1C所成角的余弦值.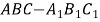

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）若函数在上是增函数，求实数的取值范围；

    （2）若存在实数使得关于的方程有三个不相等的实数根，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，、分别为椭圆的左、右焦点.设不经过焦点的直线与椭圆交于两个不同的点、，焦点到直线的距离为.若直线、、的斜率依次成等差数列，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}为等差数列，数列{an}，{bn}满足a1=b1=2，b2=6，且an+1bn=anbn+bn+1．

    （1）求{an}的通项公式；

    （2）求{bn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，O为原点，两个点列 和 满足：① ；②

    （1）求点和的坐标；

    (2)求向量的坐标；

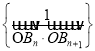    （3）对于正整数k，用表示无穷数列 中从第k+1项开始的各项之和，用表示无穷数列 中从第k项开始的各项之和，即, 若存在正整数k和p，使得，求k,p的值.

    查看答案和解析>>

    同步练习册答案