解:(I)若m=0,n=1,由已知函数f(x)=
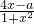
在区间[0,1]上为增函数,
可得 f′(x)=
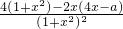
=

在区间[0,1]上恒正,
故有

,解得a≥0,故实数a的取值范围为[0,+∞).
(Ⅱ)(i)因为f(n)-f(m)=f(n)+[-f(m)]≥2

=2
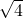
=4,当且仅当f(n)=-f(m)=2时等号成立.
由f(n)=

,有-a=2(n-1)
2≥0,得a≤0; 由f(m)=
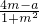
,有a=2(m+1)
2≥0,得a≥0;
故f(n)-f(m)取得最小值时,a=0,n=1.
(ii)此时,f′(x
0)=
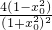
,
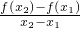
=
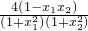
,
由f′(x
0)=
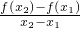
,可得

=

.
欲证x
1<x
0<x
2,先比较

与

的大小.
由于

-

=

-

=

=

.
因为0<x
1<x
2<1,所以0<x
1x
2<1,有x
1(2-x
1x
2)+x
2>0,
于是(x
1-x
2)[x
1(2-x
1x
2)+x
2]<0,即

-

<0.
另一方面,

-

=
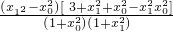
,
因为0<x
12x
02<1,所以3+x
12+x
02-x
12x
02>0,从而x
12-x
02<0,即x
1<|x
0|.
同理可证x
0<x
2,因此x
1<|x
0|<x
2.
分析:(I)由题意可得可得 f′(x)=
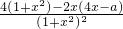
=

在区间[0,1]上恒正,故有

,由此求得实数a的取值范围
(Ⅱ)(i)因为f(n)-f(m)=f(n)+[-f(m)]≥2

=2
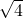
=4,当且仅当f(n)=-f(m)=2时等号成立,由此求得a的值.
(ii)先求得f′(x
0)=
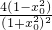
,
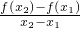
=
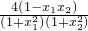
,可得

=

.欲证x
1<x
0<x
2,先用作差法求得

<

.另一方面,根据

-

=
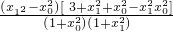
,可得x
12-x
02<0,即x
1<|x
0|.
同理可证x
0<x
2,因此x
1<|x
0|<x
2.
点评:本题主要考查导数在研究单调性,求最值,比较大小中的应用,属于中档题.

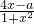 在区间[m,n]上为增函数,
在区间[m,n]上为增函数,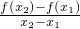 ,证明:x1<x0<x2.
,证明:x1<x0<x2.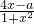 在区间[0,1]上为增函数,
在区间[0,1]上为增函数,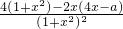 =
= 在区间[0,1]上恒正,
在区间[0,1]上恒正, ,解得a≥0,故实数a的取值范围为[0,+∞).
,解得a≥0,故实数a的取值范围为[0,+∞). =2
=2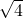 =4,当且仅当f(n)=-f(m)=2时等号成立.
=4,当且仅当f(n)=-f(m)=2时等号成立. ,有-a=2(n-1)2≥0,得a≤0; 由f(m)=
,有-a=2(n-1)2≥0,得a≤0; 由f(m)=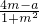 ,有a=2(m+1)2≥0,得a≥0;
,有a=2(m+1)2≥0,得a≥0;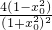 ,
,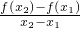 =
=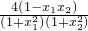 ,
,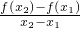 ,可得
,可得  =
= .
. 与
与  的大小.
的大小. -
- =
= -
- =
= =
= .
. -
- <0.
<0. -
- =
=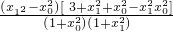 ,
,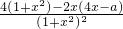 =
= 在区间[0,1]上恒正,故有
在区间[0,1]上恒正,故有 ,由此求得实数a的取值范围
,由此求得实数a的取值范围 =2
=2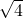 =4,当且仅当f(n)=-f(m)=2时等号成立,由此求得a的值.
=4,当且仅当f(n)=-f(m)=2时等号成立,由此求得a的值.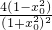 ,
,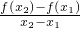 =
=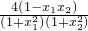 ,可得
,可得  =
= .欲证x1<x0<x2,先用作差法求得
.欲证x1<x0<x2,先用作差法求得  <
< .另一方面,根据
.另一方面,根据  -
- =
=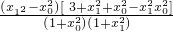 ,可得x12-x02<0,即x1<|x0|.
,可得x12-x02<0,即x1<|x0|.
