
【题目】如图所示,在五面体![]() 中,四边形
中,四边形![]() 为菱形,且
为菱形,且![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)取BD中点O,连接OM,OE,通过证明四边形OMEF为平行四边形得出FM∥OE,故而FM∥平面BDE;(2)取AD的中点H,证明EH⊥平面ABCD,由(1)得![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离.所以
的距离.所以![]() ,求出
,求出![]() 即可.
即可.
证明:(1)取![]() 中点
中点![]() ,连接
,连接![]() ,因为
,因为![]() 分别为
分别为![]() 中点,
中点,
所以![]() 且
且![]() ,
,
由已知![]() 且
且![]() ,又在菱形
,又在菱形![]() 为菱形中,
为菱形中,![]() 与
与![]() 平行且相等,所以
平行且相等,所以![]() 且
且![]() . 所以
. 所以![]() 且
且![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
又![]() 平面
平面![]() 且
且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
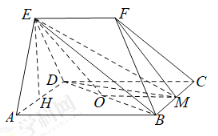
(2)由(1)得![]() 平面
平面![]() ,
,
所以![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离.
的距离.
取![]() 的中点
的中点![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
由已知可得![]() 是边长为4的等边三角形,故
是边长为4的等边三角形,故![]() ,
,
又因为![]()
![]()


科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB![]() EF,矩形ABCD所在平面和圆O所在平面垂直,已知AB=2,EF=1.
EF,矩形ABCD所在平面和圆O所在平面垂直,已知AB=2,EF=1.
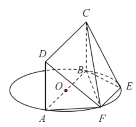
(I)求证:平面DAF⊥平面CBF;
(II)若BC=1,求四棱锥F-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:
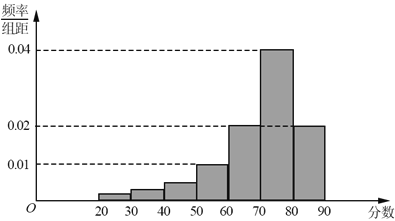
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M点为圆心的圆![]() 及其上一点
及其上一点![]() .
.

(1)设圆N与y轴相切,与圆M外切,且圆心在直线![]() 上,求圆N的标准方程;
上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B,C两点且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所抽取的30岁以上的网友中利用分层抽样的方法再抽取5人.
(i)分别求这5人中经常使用、偶尔或不用共享单车的人数;
(ii)从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生小王自主创业,在乡下承包了一块耕地种植某种水果,每季投入2万元,根据以往的经验,每季收获的此种水果能全部售完,且水果的市场价格和这块地上的产量具有随机性,互不影响,具体情况如表:

(Ⅰ)设![]() 表示在这块地种植此水果一季的利润,求
表示在这块地种植此水果一季的利润,求![]() 的分布列及期望;
的分布列及期望;
(Ⅱ)在销售收入超过5万元的情况下,利润超过5万元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com