练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在区间上任取一个数记为a，在区间上任取一个数记为b．

    若a，，求直线的斜率为的概率；

    若a，，求直线的斜率为的概率．

    【答案】（1）；（2）.

    【解析】

    ，2，3，4，5，6，，2，3，4，5，基本事件总数，再列出满足条件的基本事件有6个，由古典概型概率计算公式求解；

    有序实数对满足，而满足直线的斜率为，即，画出图形，由测度比是面积比得答案．

    解：在区间上任取一个数记为a，在区间上任取一个数记为b，

    a，，，2，3，4，5，6，，2，3，4，5．

    基本事件总数，

    直线的斜率为，即，也就是，

    满足条件的基本事件有6个，分别是：

    ，，，，，，

    直线的斜率为的概率；

    在区间上任取一个数记为a，在区间上任取一个数记为b，a，，

    有序实数对满足，

    而满足直线的斜率为，即，

    如图：，．

    直线的斜率为的概率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PB、PD与平面ABCD所成角的正切值依次是1、，AP＝2，E、F依次是PB、PC的中点．

    (1)求证：PB⊥平面AEFD；

    (2)求直线EC与平面PAD所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某渔业公司年初用81万元购买一艘捕鱼船，第一年各种费用为1万元，以后每年都增加2万元，每年捕鱼收益30万元．

    问第几年开始获利？

    若干年后，有两种处理方案：方案一：年平均获利最大时，以46万元出售该渔船；

    方案二：总纯收入获利最大时，以10万元出售该渔船问：哪一种方案合算？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在凸四边形ABCD中，AB=1，BC= ，AC⊥DC，CD= AC．设∠ABC=θ．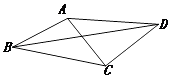

    （1）若θ=30°，求AD的长；
    （2）当θ变化时，求BD的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）在定义域[2﹣a，3]上是偶函数，在[0，3]上单调递增，并且f（﹣m2﹣ ）＞f（﹣m2+2m﹣2），则m的取值范围是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，，，平面ABC．

    若，求直线与平面所成的角的大小；

    在的条件下，求二面角的大小；

    若，平面，G为垂足，令其中p、q、，求p、q、r的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设△ABC的内角A，B，C的对边分别为a、b、c，a=btanA，且B为钝角．
    （1）证明：B﹣A= ；
    （2）求sinA+sinC的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数为定义域上的奇函数，且在上是单调递增函数，函数，数列为等差数列，，且公差不为0，若，则（ ）

    A. 45 B. 15 C. 10 D. 0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点在抛物线上，则当点到点的距离与点到抛物线焦点距离之和取得最小值时，点的坐标为（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案