
分析 首先,将点P的坐标代入,得到所求角的取值,然后,在图形中标注即可.
解答  解:∵点P(4,-$\frac{12}{5}$)在椭圆上,
解:∵点P(4,-$\frac{12}{5}$)在椭圆上,
∴$\left\{\begin{array}{l}{4=5cosθ}\\{-\frac{12}{5}=4sinθ}\end{array}\right.$,
∴$\left\{\begin{array}{l}{sinθ=-\frac{3}{5}}\\{cosθ=\frac{4}{5}}\end{array}\right.$,
∵sinθ<0,cosθ>0,
∴θ=2π-arctan$\frac{3}{4}$,
如下图所示:
点评 本题重点考查了椭圆的参数方程及其应用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
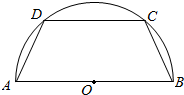 如图所示,半径为R的圆的内接等腰梯形ABCD的下底AB是圆O的直径,上底CD的端点在圆周上,建立这个梯形的周长y与腰长x的解析式,并求出它的定义域函数解析式,并求出它的定义域.
如图所示,半径为R的圆的内接等腰梯形ABCD的下底AB是圆O的直径,上底CD的端点在圆周上,建立这个梯形的周长y与腰长x的解析式,并求出它的定义域函数解析式,并求出它的定义域.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com