
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作平面
作平面![]() 的垂线,垂足为
的垂线,垂足为![]() 与
与![]() 的交点
的交点![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
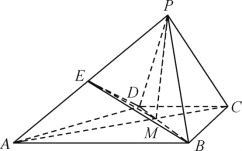
(1)求证:DE//平面![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,根据中位线定理可知
,根据中位线定理可知![]() 且
且![]() ,根据题意可得
,根据题意可得![]() 且
且![]() ,进一步可知
,进一步可知![]() ,然后根据线面平行的判定定理,可得结果.
,然后根据线面平行的判定定理,可得结果.
(2)根据四棱锥![]() 的体积,可得
的体积,可得![]() ,通过建立空间直角坐标系,求得
,通过建立空间直角坐标系,求得![]() ,并得到平面
,并得到平面![]() 的一个法向量,然后简单计算,可得结果.
的一个法向量,然后简单计算,可得结果.
证明:(1)取![]() 的中点
的中点![]() ,分别连接
,分别连接![]() ,
,
如图
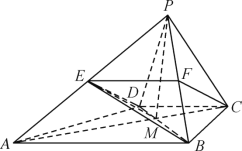
因为![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,
的中点,
所以![]() 是
是![]() 的中位线,
的中位线,
所以![]() 且
且![]() .
.
在平面![]() 内
内![]() ,
,![]() 知,
知,![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() //
//![]() ,且
,且![]() .
.
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)以点![]() 为原点,以平行于
为原点,以平行于![]() 的直线为
的直线为![]() 轴,
轴,
以平行于![]() 的直线为
的直线为![]() 轴,以直线
轴,以直线![]() 为
为![]() 轴,
轴,
建立如下图所示的空间直角坐标系.
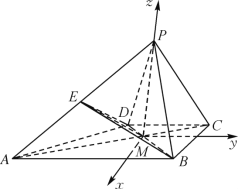
设点![]() ,则
,则![]() ,
,![]() .
.
所以有点![]() .
.
因为四棱锥![]() 的体积为
的体积为![]() ,
,
所以![]() ,解得
,解得![]() ,则
,则![]() .
.
又![]() 为
为![]() 中点知,则点
中点知,则点![]() 坐标为
坐标为![]() .
.
又点![]() 的坐标是
的坐标是![]() ,所以
,所以![]() .
.
平面![]() 的一个法向量
的一个法向量![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则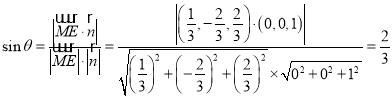 .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】2019年4月10日21时整,全球六地(上海和台北、布鲁塞尔、圣地亚哥、东京和华盛顿同时召开新闻发布会,宣布人类首次利用虚拟射电望远镜,成功捕获世界上首张黑洞图像,公布的照片展示了一个中心为黑色的明亮环状结构,看上去有点像个橙色的甜甜圈,其黑色部分是黑洞投下的“阴影”,明亮部分是绕黑洞高速旋转的吸积盘.某同学作了一张黑洞示意图,如图所示,由两个同心圆和半个同心圆环构成圆及圆环的半径从内到外依次为2,3,4,5个单位在图中随机任取一点,则该点取自阴影的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为A,高和底面的半径相等,BE是底面圆的一条直径,点D为底面圆周上的一点,且∠ABD=60°,则异面直线AB与DE所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为
(θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)求曲线C1的极坐标方程以及曲线C2的直角坐标方程;
(2)若直线l:y=kx与曲线C1、曲线C2在第一象限交于P、Q,且|OQ|=|PQ|,点M的直角坐标为(1,0),求△PMQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,侧面SCD为钝角三角形且垂直于底面ABCD,CD=SD,点M是SA的中点,AD//BC,∠ABC=90°,AB=AD![]() BC=a.
BC=a.
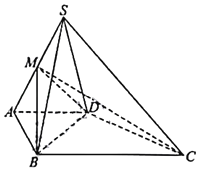
(1)求证:平面MBD⊥平面SCD;
(2)若∠SDC=120°,求三棱锥C﹣MBD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,棱长为2,
中,棱长为2,![]() 分别为棱
分别为棱![]() 的中点,
的中点,![]() 为底面正方形
为底面正方形![]() 内一点(含边界)且
内一点(含边界)且![]() 与面
与面![]() 所成角的正切值为
所成角的正切值为![]() ,直线
,直线![]() 与面
与面![]() 的交点为
的交点为![]() ,当
,当![]() 到
到![]() 的距离最小时,则四面体
的距离最小时,则四面体![]() 外接球的表面积为___________.
外接球的表面积为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),若以O为极点,x轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线C的极坐标方程为
(t为参数),若以O为极点,x轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求曲线C的直角坐标方程及直线l的普通方程;
(2)将所得曲线C向右平移1个单位长度,再将曲线C上的所有点的横坐标变为原来的2倍,得到曲线![]() ,求曲线
,求曲线![]() 上的点到直线l的距离的最大值.
上的点到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为![]() 和
和![]() 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为![]() ,宽为内接正方形的边长
,宽为内接正方形的边长![]() .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设![]() 为斜边
为斜边![]() 的中点,作直角三角形
的中点,作直角三角形![]() 的内接正方形对角线
的内接正方形对角线![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则下列推理正确的是( )
,则下列推理正确的是( )
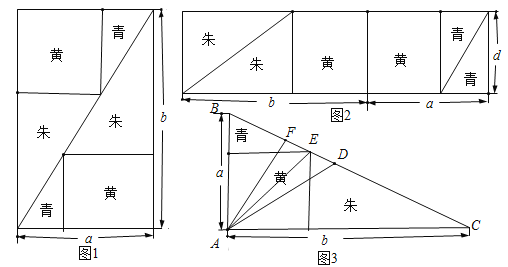
①由图1和图2面积相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得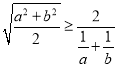 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设点![]() 是抛物线
是抛物线![]() 的焦点,直线
的焦点,直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() (点
(点![]() 位于第一象限),并与抛物线
位于第一象限),并与抛物线![]() 的准线相交于点
的准线相交于点![]() .过点
.过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,连结
,连结![]() .
.
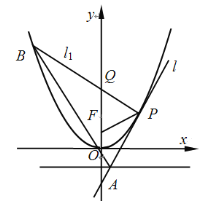
(1)证明:![]() 为等腰三角形;
为等腰三角形;
(2)求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com