
【题目】已知点![]() 、
、![]() 为双曲线
为双曲线![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴上方交双曲线
轴上方交双曲线![]() 于点
于点![]() ,且
,且![]() .
.

(1)求双曲线![]() 的两条渐近线的夹角
的两条渐近线的夹角![]() ;
;
(2)过点![]() 的直线
的直线![]() 和双曲线
和双曲线![]() 的右支交于
的右支交于![]() 、
、![]() 两点,求
两点,求![]() 的面积的最小值;
的面积的最小值;
(3)过双曲线![]() 上任意一点
上任意一点![]() 分别作该双曲线两条渐近线的平行线,它们分别交两条渐近线于
分别作该双曲线两条渐近线的平行线,它们分别交两条渐近线于![]() 、
、![]() 两点,求平行四边形
两点,求平行四边形![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)首先根据双曲线的定义,结合题中所给的角的大小,求得![]() ,从而求得b的值,进而得到双曲线的渐近线方程,利用直线的方向向量所成的角,求得两条渐近线的夹角余弦值,利用反余弦求出结果;
,从而求得b的值,进而得到双曲线的渐近线方程,利用直线的方向向量所成的角,求得两条渐近线的夹角余弦值,利用反余弦求出结果;
(2)设出直线的方程,与双曲线的方程联立,利用三角形的面积公式,结合函数的单调性,求得最值,得到结果;
(3)根据所学的知识将四边形的面积表示出来,进而求得结果.
(1)由题意,得![]() ,
,
![]() ,
,
∴![]() ,∴双曲线
,∴双曲线![]() 的方程为
的方程为![]() ,
,
∴![]() ,∴
,∴![]() ;
;
(2)【注:若设点斜式,需补上斜率不存在的情况】
设![]() ,
,![]() 、
、![]() ,
,
将直线![]() 的方程代入双曲线方程,消去
的方程代入双曲线方程,消去![]() ,得
,得![]() ,
,
则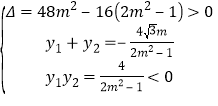 ,得
,得![]() ,
,
![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,
,
其中![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,此时
,此时![]() ,
,![]() 的方程为
的方程为![]() ;
;
(3)设![]() ,其中
,其中![]()
方法一:设![]() ,与
,与![]() 联立,
联立,
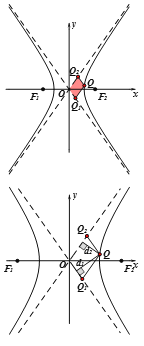
可求出![]() ,
,
由三阶行列式表示的三角形面积公式
可得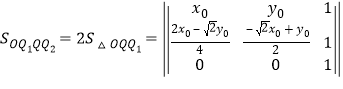
![]() .
.
方法二:如图,![]() ,
,![]()
设![]() 到
到![]() 和
和![]() 的距离为
的距离为![]() 、
、![]() ,
,
则![]() ,
,![]() ,
,
∴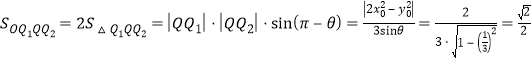


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,两焦点分别为
,两焦点分别为![]() ,右顶点为
,右顶点为![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过定点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 的左支有两个交点,与椭圆
的左支有两个交点,与椭圆![]() 交于
交于![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,
, ![]() ,求正数
,求正数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王在年初用50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小王在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售价格为25-x万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小王获得的年平均利润最大(利润=累计收入+销售收入-总支出)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,斜率为1的直线l交椭圆于A、B两点,且线段AB的中点坐标为
,斜率为1的直线l交椭圆于A、B两点,且线段AB的中点坐标为![]() .
.
![]() 求椭圆的方程;
求椭圆的方程;
![]() 若P是椭圆与双曲线
若P是椭圆与双曲线![]() 在第一象限的交点,求
在第一象限的交点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将一矩形花坛![]() 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛![]() ,要求
,要求![]() 点在
点在![]() 上,
上,![]() 点在
点在![]() 上,且对角线
上,且对角线![]() 过
过![]() 点,已知
点,已知![]() 米,
米,![]() 米.
米.

(1)要使矩形![]() 的面积大于
的面积大于![]() 平方米,则
平方米,则![]() 的长应在什么范围内?
的长应在什么范围内?
(2)当![]() 的长度是多少时,矩形花坛
的长度是多少时,矩形花坛![]() 的面积最小?并求出最小值.
的面积最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】意大利数学家列昂纳多·斐波那契是第一个研究了印度和阿拉伯数学理论的欧洲人,斐波那契数列被誉为是最美的数列,斐波那契数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com