
 ,曲线y=f(x)在点(2,f(2))处的切线方程为y=3.
,曲线y=f(x)在点(2,f(2))处的切线方程为y=3. 都是奇函数.可得和函数也是奇函数,其图象是以原点为中心的中心对称图形.再按向量a=(1,1)平移,即得到函数f(x)的图象,故函数f(x)的图象是以点(1,1)为中心的中心对称图形.
都是奇函数.可得和函数也是奇函数,其图象是以原点为中心的中心对称图形.再按向量a=(1,1)平移,即得到函数f(x)的图象,故函数f(x)的图象是以点(1,1)为中心的中心对称图形. .利用导数求出过此点的切线方程为,令x=1得切线与直线x=1交点.令y=x得切线与直线y=x交点.从而利用面积公式求得所围三角形的面积为定值.
.利用导数求出过此点的切线方程为,令x=1得切线与直线x=1交点.令y=x得切线与直线y=x交点.从而利用面积公式求得所围三角形的面积为定值. ,
,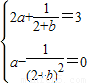
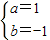 或
或
 .
. 都是奇函数.
都是奇函数. 也是奇函数,其图象是以原点为中心的中心对称图形.
也是奇函数,其图象是以原点为中心的中心对称图形. .可知,函数g(x)的图象按向量a=(1,1)平移,即得到函数f(x)的图象,
.可知,函数g(x)的图象按向量a=(1,1)平移,即得到函数f(x)的图象, .
. 知,过此点的切线方程为
知,过此点的切线方程为 .
. ,切线与直线x=1交点为
,切线与直线x=1交点为 .
. .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源:《第1章 导数及其应用》2013年单元测试卷(2)(解析版) 题型:解答题
 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.查看答案和解析>>
科目:高中数学 来源:2012-2013学年内蒙古包头33中高三(上)期中数学试卷(文科)(解析版) 题型:解答题
 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.查看答案和解析>>
科目:高中数学 来源:2011年四川省南充市高考数学一模试卷(理科)(解析版) 题型:解答题
 ,曲线y=f(x)在点(2,f(2))处的切线方程为y=3.
,曲线y=f(x)在点(2,f(2))处的切线方程为y=3.查看答案和解析>>
科目:高中数学 来源:2011年高三数学第一轮复习巩固与练习:导数及其应用(解析版) 题型:解答题
 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.查看答案和解析>>
科目:高中数学 来源:2011年高三数学(文科)一轮复习讲义:2.9 导数的概念及运算(解析版) 题型:解答题
 ,曲线y=f(x)在点(2,f(2))处的切线方程为y=3.
,曲线y=f(x)在点(2,f(2))处的切线方程为y=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com