
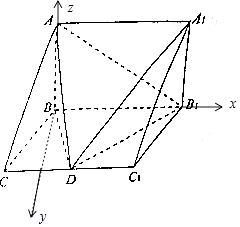
【题目】如图,在三棱柱ABC﹣A1B1C1中,AB⊥平面BB1C1C,∠BCC1= ![]() ,AB=BB1=2,BC=1,D为CC1中点.
,AB=BB1=2,BC=1,D为CC1中点. 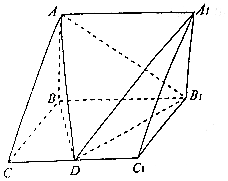
(1)求证:DB1⊥平面ABD;
(2)求二面角A﹣B1D﹣A1的平面角的余弦值.
【答案】
(1)证明:∵BC=B1C1=1,CD=C1D= ![]() BB1=1,∠BCC1=
BB1=1,∠BCC1= ![]() ,∠B1C1D=π﹣∠BCC1=
,∠B1C1D=π﹣∠BCC1= ![]() ,
,
∴BD=1,B1D= ![]() ,
,
∴BB12=BD2+B1D2,∴BD⊥B1D.
∵AB⊥平面BB1C1C,BD平面BB1C1C,
∴AB⊥B1D,又AB平面ABD,BD平面ABD,AB∩BD=B,
∴DB1⊥平面ABD
(2)解:以B为原点,以BB1,BA所在直线为x轴,z轴建立空间直角坐标系B﹣xyz,如图所示:
则A(0,0,2),D( ![]() ,
, ![]() ,0),B1(2,0,0),A1(2,0,2),
,0),B1(2,0,0),A1(2,0,2),
∴ ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,0),
,0), ![]() =(﹣2,0,2),
=(﹣2,0,2), ![]() =(0,0,2).
=(0,0,2).
设平面AB1D的法向量为 ![]() =(x1,y1,z1),平面A1B1D的法向量为
=(x1,y1,z1),平面A1B1D的法向量为 ![]() =(x2,y2,z2),
=(x2,y2,z2),
则 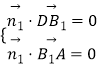 ,
, 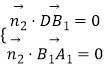 ,即
,即 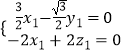 ,
, 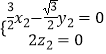 ,
,
令x1=1得 ![]() =(1,
=(1, ![]() ,1),令x2=1得
,1),令x2=1得 ![]() =(1,
=(1, ![]() ,0).
,0).
∴cos< ![]() ,
, ![]() >=
>= 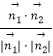 =
= ![]() =
= ![]() .
.
∵二面角A﹣B1D﹣A1是锐角,
∴二面角A﹣B1D﹣A1的平面角的余弦值为 ![]() .
.
【解析】(1)利用余弦定理计算BD,B1D,再由勾股定理的逆定理得出BD⊥B1D,由AB⊥平面BB1C1C得出AB⊥B1D,于是得出B1D⊥平面ABD;(2)以B为原点建立坐标系,求出平面AB1D的法向量 ![]() ,平面A1B1D的法向量
,平面A1B1D的法向量 ![]() ,计算cos<
,计算cos< ![]() ,
, ![]() >即可得出二面角的余弦值.
>即可得出二面角的余弦值.


科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且满足cos2B﹣cos2C﹣sin2A=sinAsimB.
(1)求角C;
(2)向量 ![]() =(sinA,cosB),
=(sinA,cosB), ![]() =(cosx,sinx),若函数f(x)=
=(cosx,sinx),若函数f(x)= ![]()
![]() 的图象关于直线x=
的图象关于直线x= ![]() 对称,求角A,B.
对称,求角A,B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,侧面PAB⊥底面ABCD,△PAB为正三角形.AB⊥AD,CD⊥AD,点E、M为线段BC、AD的中点,F,G分别为线段PA,AE上一点,且AB=AD=2,PF=2FA. 
(1)确定点G的位置,使得FG∥平面PCD;
(2)试问:直线CD上是否存在一点Q,使得平面PAB与平面PMQ所成锐二面角的大小为30°,若存在,求DQ的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在抛物线
在抛物线![]()
![]() 上,
上, ![]() 点到抛物线
点到抛物线![]() 的焦点
的焦点![]() 的距离为2,直线
的距离为2,直线
![]()
![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.
(1)求抛物线![]() 的方程;
的方程;
(2)若以![]() 为直径的圆与
为直径的圆与![]() 轴相切,求该圆的方程.
轴相切,求该圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的方程为 ![]() ,⊙C的极坐标方程为ρ=4cosθ+2sinθ.
,⊙C的极坐标方程为ρ=4cosθ+2sinθ.
(1)求直线l和⊙C的普通方程;
(2)若直线l与圆⊙C交于A,B两点,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() 分别为双曲线
分别为双曲线![]() 的左、右焦点,
的左、右焦点, ![]() 为双曲线的左顶点,以
为双曲线的左顶点,以![]() ,
, ![]() 为直径的圆交双曲线某条渐近线于
为直径的圆交双曲线某条渐近线于![]() ,
, ![]() 两点,且满足
两点,且满足![]() ,则该双曲线的离心率为________.
,则该双曲线的离心率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com