
分析 不等式可因式分解为(ax+1)(x-1)>0,
由a<0,左右两边同时除以a,得$[{x-(-\frac{1}{a})}](x-1)<0$,
进而讨论$-\frac{1}{a}$和1的大小,写出对应的解集.
解答 解:不等式ax2+(2-a)x-2>0可化为(ax+1)(x-1)>0,
∵a<0,左右两边同时除以a,得
$[{x-(-\frac{1}{a})}](x-1)<0$,
比较$-\frac{1}{a}$和1的大小,得:
①当-1<a<0时,∵$-\frac{1}{a}>1$,且原不等式可化为$[{x-(-\frac{1}{a})}](x-1)<0$,
∴其解集为$\left\{{x|1<x<-\frac{1}{a}}\right\}$;
②当a=-1时,∵$1=-\frac{1}{a}$,且原不等式可化为(x-1)2<0,其解集为∅;
③当a<-1时,∵$1>-\frac{1}{a}$,且原不等式可化为$[{x-(-\frac{1}{a})}](x-1)<0$,
∴其解集为$\left\{{x|-\frac{1}{a}<x<1}\right\}$;
综上:当-1<a<0时,解集为$\left\{{x|1<x<-\frac{1}{a}}\right\}$;
当时a=-1,解集为∅;
当a<-1时,解集为$\left\{{x|-\frac{1}{a}<x<1}\right\}$.
点评 本题考查了用分类讨论法求含有字母系数的一元二次不等式的问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
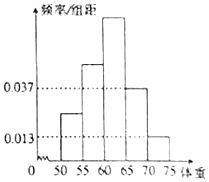 为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.
为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9π,12π | B. | 12π,9π | C. | 24π,12π | D. | 15π,36π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36 | B. | 35 | C. | 32 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
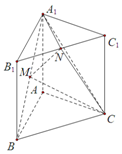 如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,AA1=2,点M,N分别为A1B和B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,AA1=2,点M,N分别为A1B和B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{49}{6}$ | B. | $\frac{25}{6}$ | C. | $\frac{8}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-5)>f(3) | B. | f(-5)<f(3) | C. | f(-3)>f(-5) | D. | f(-3)<f(-5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com