
【题目】[选修4-5:不等式选讲]已知函数f(x)=|x﹣a|+|2x﹣1|(a∈R).
(Ⅰ)当a=1时,求f(x)≤2的解集;
(Ⅱ)若f(x)≤|2x+1|的解集包含集合[ ![]() ,1],求实数a的取值范围.
,1],求实数a的取值范围.
【答案】解:( I)当a=1时,f(x)=|x﹣1|+|2x﹣1|,f(x)≤2|x﹣1|+|2x﹣1|≤2, 上述不等式可化为 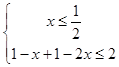 或
或  或
或 ![]()
解得 ![]() 或
或  或
或 ![]()
∴ ![]() 或
或 ![]() 或
或 ![]() ,
,
∴原不等式的解集为 ![]() .
.
( II)∵f(x)≤|2x+1|的解集包含 ![]() ,
,
∴当 ![]() 时,不等式f(x)≤|2x+1|恒成立,
时,不等式f(x)≤|2x+1|恒成立,
即|x﹣a|+|2x﹣1|≤|2x+1|在 ![]() 上恒成立,
上恒成立,
∴|x﹣a|+2x﹣1≤2x+1,
即|x﹣a|≤2,∴﹣2≤x﹣a≤2,
∴x﹣2≤a≤x+2在 ![]() 上恒成立,
上恒成立,
∴(x﹣2)max≤a≤(x+2)min , ∴ ![]() ,
,
所以实数a的取值范围是 ![]()
【解析】( I)运用分段函数求得f(x)的解析式,由f(x)≤2,即有 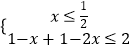 或
或  或
或 ![]() ,解不等式即可得到所求解集;(Ⅱ)由题意可得当
,解不等式即可得到所求解集;(Ⅱ)由题意可得当 ![]() 时,不等式f(x)≤|2x+1|恒成立.即有(x﹣2)max≤a≤(x+2)min . 求得不等式两边的最值,即可得到a的范围.
时,不等式f(x)≤|2x+1|恒成立.即有(x﹣2)max≤a≤(x+2)min . 求得不等式两边的最值,即可得到a的范围.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1经过点(2,3),两条渐近线的夹角为60°,直线l交双曲线于A,B两点.
=1经过点(2,3),两条渐近线的夹角为60°,直线l交双曲线于A,B两点.
(1)求双曲线C的方程;
(2)若l过原点,P为双曲线上异于A,B的一点,且直线PA,PB的斜率kPA , kPB均存在,求证:kPAkPB为定值;
(3)若l过双曲线的右焦点F1 , 是否存在x轴上的点M(m,0),使得直线l绕点F1无论怎样转动,都有 ![]() =0成立?若存在,求出M的坐标;若不存在,请说明理由.
=0成立?若存在,求出M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=lg(m2﹣2m﹣2)+(m2+3m+2)i,根据以下条件分别求实数m的值或范围.
(1)z是纯虚数;
(2)z对应的点在复平面的第二象限.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图所示的程序框图 
(1)当输入的x为2,﹣1时,分别计算输出的y值,并写出输出值y关于输入值x的函数关系式;
(2)当输出的结果为4时,求输入的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年上半年,股票投资人袁先生同时投资了甲、乙两只股票,其中甲股票赚钱的概率为 ![]() ,赔钱的概率是
,赔钱的概率是 ![]() ;乙股票赚钱的概率为
;乙股票赚钱的概率为 ![]() ,赔钱的概率为
,赔钱的概率为 ![]() .对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元. (Ⅰ)求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;
.对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元. (Ⅰ)求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;
(Ⅱ)试求袁先生2016年上半年同事投资甲、乙两只股票的总收益的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量X﹣N(1,1),其正态分布密度曲线如图所示,若向正方形OABC中随机投掷10000个点,则落入阴影部分的点个数的估计值为( ) 附:若随机变量ξ﹣N(μ,σ2),则P(μ﹣σ<ξ≤μ+σ)=0.6826,P(μ﹣2σ<ξ≤μ+2σ)=0.9544.
A.6038
B.6587
C.7028
D.7539
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2, ![]() cos2B+5cosB﹣
cos2B+5cosB﹣ ![]() =0,且点D在线段BC上.
=0,且点D在线段BC上. 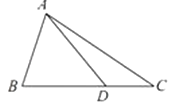
(1)若∠ADC= ![]() ,求AD的长;
,求AD的长;
(2)若BD=2DC, ![]() =4
=4 ![]() ,求△ABD的面积.
,求△ABD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax+ ![]() ,且f(x)+f(
,且f(x)+f( ![]() )=0,其中a,b为常数.
)=0,其中a,b为常数.
(1)若函数f(x)的图象在x=1的切线经过点(2,5),求函数的解析式;
(2)已知0<a<1,求证:f( ![]() )>0;
)>0;
(3)当f(x)存在三个不同的零点时,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com