
三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC。

(1)证明:平面PAB⊥平面PBC;
(2)若 ,
,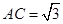 ,PB与底面ABC成60°角,
,PB与底面ABC成60°角,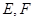 分别是
分别是 与
与 的中点,
的中点, 是线段
是线段 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体 的体积。
的体积。
【解析】
试题分析:(Ⅰ)先利用线面垂直的判定定理证明BC⊥平面PAB,再利用面面垂直的判定定理证明平面PAB⊥平面PBC;(2)由已知条件在在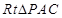 中,计算可得
中,计算可得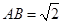 ,可证
,可证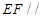 面
面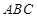 ,即点S到平面ABC的距离是PA的一半,最后根据棱锥的体积公式计算即可.
,即点S到平面ABC的距离是PA的一半,最后根据棱锥的体积公式计算即可.
试题解析:17、(1)证明:∵PA^面ABC,\PA^BC,
∵AB^BC,且PA∩AB=A,\BC^面PAB
而BCÌ面PBC中,\面PAB^面PBC. 5分
(2)解:PB与底面ABC成60°角,
即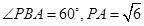 , 6分
, 6分
在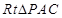 中,
中,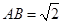 ,又
,又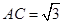 ,
,
在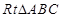 中,
中,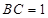 。 8分
。 8分
E、F分别是PB与PC的中点,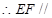 面
面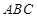 9分
9分
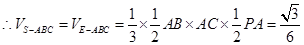 12分
12分
考点:1.平面与平面垂直的判定;2.直线与平面所成的角和二面角.3.棱锥的体积.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源:2013-2014学年四川成都外国语学校高三12月月考理科数学试卷(解析版) 题型:解答题
三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC。
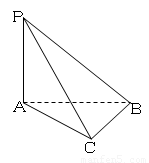
(1)证明:平面PAB⊥平面PBC;
(2)若PA=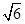 ,PC与侧面APB所成角的余弦值为
,PC与侧面APB所成角的余弦值为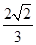 ,PB与底面ABC成60°角,求二面角B―PC―A的大小。
,PB与底面ABC成60°角,求二面角B―PC―A的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com