
【题目】某大型超市抽查了100天该超市的日纯利润数据,并将日纯利润数据分成以下几组(单位:万元):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,统计结果如下表所示:
,统计结果如下表所示:
组别 |
|
|
|
|
|
|
频数 | 5 | 20 | 30 | 30 | 10 | 5 |
以上述样本分布的频率估计总体分布的概率,解决下列问题:
(1)从该大型超市近几年的销售记录中抽出5天,求其中日纯利润在区间![]() 内的天数不少于2的概率;
内的天数不少于2的概率;
(2)该超市经理由频数分布表可以认为,该大型超市每天的纯利润![]() 服从正态分布
服从正态分布![]() ,其中,
,其中,![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值).
(每组数据取区间的中点值).
①试利用该正态分布,估计该大型超市1000天内日纯利润在区间![]() 内的天数(精确到个位);
内的天数(精确到个位);
②该大型超市负责人根据每日的纯利润给超市员工制定了两种不同的奖励方案:
方案一:直接发放奖金,日纯利润低于![]() 时每名员工发放奖金70元,日纯利润不低于
时每名员工发放奖金70元,日纯利润不低于![]() 时每名员工发放奖金90元;
时每名员工发放奖金90元;
方案二:利用抽奖的方式获得奖金,其中日纯利润不低于![]() 时每位员工均有两次抽奖机会,日纯利润低于
时每位员工均有两次抽奖机会,日纯利润低于![]() 时每位员工只有一次抽奖机会;每次抽奖的奖金及对应的概率分别为
时每位员工只有一次抽奖机会;每次抽奖的奖金及对应的概率分别为
金额 | 50元 | 100元 |
概率 |
|
|
小张恰好为该大型超市的一名员工,则从数学期望的角度看,小张选择哪种奖励方案更有利?
参考数据:若![]() ,则
,则![]() ,
,![]() .
.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②奖励方案二.
;②奖励方案二.
【解析】
(1)由频数分布表可知,日纯利润在区间![]() 内的频率为
内的频率为![]() ,基于“用样本频率估计总体分布的概率”的思想,可知日纯利润在区间
,基于“用样本频率估计总体分布的概率”的思想,可知日纯利润在区间![]() 内的频率为
内的频率为![]() ,记其中日纯利润不低于5万元且低于7万元的天数为
,记其中日纯利润不低于5万元且低于7万元的天数为![]() ,则
,则![]() ,基于二项分布的性质即可求解;
,基于二项分布的性质即可求解;
(2)①基于正态分布的![]() 原则及其性质即可求解;
原则及其性质即可求解;
②首先计算方案一的数学期望,其次针对方案二,列出随机变量![]() 的分布列,计算出方案二的数学期望,比较两方案的结果,判断出选择方案二更有利.
的分布列,计算出方案二的数学期望,比较两方案的结果,判断出选择方案二更有利.
(1)由频数分布表可知,日纯利润在区间![]() 内的频率为
内的频率为![]() ,
,
记其中日纯利润不低于5万元且低于7万元的天数为![]() ,则
,则![]() .
.
![]() 所求的概率
所求的概率![]()
![]() .
.
(2)①![]()
![]() ,
,![]() .又
.又![]() ,
,
![]()
![]()
![]()
![]()
![]() .
.
故该大型超市1000天内日纯利润在区间![]() 的天数为
的天数为![]() .
.
②易知![]() .
.
对于奖励方案一:设小张每日奖金金额为![]() ,则
,则![]() 的可能取值为70,90,其对应的概率均为
的可能取值为70,90,其对应的概率均为![]() ,故
,故![]() .
.
对于奖励方案二:设小张每日奖金金额为![]() ,则
,则![]() 的所有可能取值为50,100,150,200.
的所有可能取值为50,100,150,200.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() 的分布列为
的分布列为
| 50 | 100 | 150 | 200 |
|
|
|
|
|
![]()
![]() .
.![]() ,
,
![]() 从数学期望的角度看,小张选择奖励方案二更有利.
从数学期望的角度看,小张选择奖励方案二更有利.


科目:高中数学 来源: 题型:
【题目】华为董事会决定投资开发新款软件,估计能获得![]() 万元到
万元到![]() 万元的投资收益,讨论了一个对课题组的奖励方案:奖金
万元的投资收益,讨论了一个对课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过投资收益的
万元,同时奖金不超过投资收益的![]() .
.
(1)请分析函数![]() 是否符合华为要求的奖励函数模型,并说明原因;
是否符合华为要求的奖励函数模型,并说明原因;
(2)若华为公司采用模型函数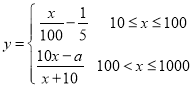 作为奖励函数模型,试确定正整数
作为奖励函数模型,试确定正整数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一名高二学生盼望2020年进入某名牌大学学习,假设该名牌大学有以下条件之一均可录取:①2020年2月通过考试进入国家数学奥赛集训队(集训队从2019年10月省数学竞赛一等奖中选拔):②2020年3月自主招生考试通过并且达到2020年6月高考重点分数线,③2020年6月高考达到该校录取分数线(该校录取分数线高于重点线),该学生具备参加省数学竞赛、自主招生和高考的资格且估计自己通过各种考试的概率如下表
省数学竞赛一等奖 | 自主招生通过 | 高考达重点线 | 高考达该校分数线 |
0.5 | 0.6 | 0.9 | 0.7 |
若该学生数学竞赛获省一等奖,则该学生估计进入国家集训队的概率是0.2.若进入国家集训队,则提前录取,若未被录取,则再按②、③顺序依次录取:前面已经被录取后,不得参加后面的考试或录取.(注:自主招生考试通过且高考达重点线才能录取)
(Ⅰ)求该学生参加自主招生考试的概率;
(Ⅱ)求该学生参加考试的次数![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)求该学生被该校录取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上的动点,给出下列说法:①
上的动点,给出下列说法:①![]() 与
与![]() 所成的最大角为
所成的最大角为![]() ;②
;②![]() 的最小值为
的最小值为![]() ;③
;③![]() 与
与![]() 垂直;④若
垂直;④若![]() 为
为![]() 的中点,则四面体
的中点,则四面体![]() 的体积为
的体积为![]() .其中正确的个数有( )
.其中正确的个数有( )

A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型超市抽查了100天该超市的日纯利润数据,并分成了以下几组(单位:万元):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .统计结果如下表所示(统计表中每个小组取中间值作为该组数据的替代值):
.统计结果如下表所示(统计表中每个小组取中间值作为该组数据的替代值):
组别 |
|
|
|
|
|
|
频数 | 5 | 20 | 30 | 30 | 10 | 5 |
(1)求这100天该大型超市日纯利润的平均数及中位数;
(2)该天型超市负责人决定利用分层抽样的方法从前2组中随机抽出5天数据分析日纯利润较少的原因,并从这5天数据中再抽出其中2天数据进行深入分析,求这2天的数据恰好来自不同组的概率;
(3)利用上述样本分布估计总体分布,解决下面问题:该大型超市总经理根据每天的纯利润给员工制定了两种奖励方案:
方案一:记日纯利润为![]() 万元,当
万元,当![]() 时,奖励每位员工40元/天;当
时,奖励每位员工40元/天;当![]() 时,奖励每位员工80元/天;当
时,奖励每位员工80元/天;当![]() 时,奖励每位员工120元/天;
时,奖励每位员工120元/天;
方案二:日纯利润低于总体中位数时每名员工发放奖金50元/天,日纯利润不低于总体中位数时每名员工发放80元奖金/天;
“小张恰好为该大型超市的一位员工,则从统计角度看,小张选择哪种奖励方案更有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(1﹣sinx)ex.
(1)求f(x)在区间(0,π)的极值;
(2)证明:函数g(x)=f(x)﹣sinx﹣1在区间(﹣π,π)有且只有3个零点,且之和为0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解市民对开设传统文化课的态度,教育机构随机抽取了![]() 位市民进行了解,发现支持开展的占
位市民进行了解,发现支持开展的占![]() ,在抽取的男性市民
,在抽取的男性市民![]() 人中持支持态度的为
人中持支持态度的为![]() 人.
人.
(1)完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为性别与支持与否有关?
的把握认为性别与支持与否有关?
支持 | 不支持 | 合计 | |
男性 | |||
女性 | |||
合计 |
(2)为了进一步征求对开展传统文化的意见和建议,从抽取的![]() 位市民中对不支持的按照分层抽样的方法抽取
位市民中对不支持的按照分层抽样的方法抽取![]() 位市民,并从抽取的
位市民,并从抽取的![]() 人中再随机选取
人中再随机选取![]() 人进行座谈,求选取的
人进行座谈,求选取的![]() 人恰好为
人恰好为![]() 男
男![]() 女的概率.
女的概率.
附: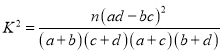
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国铁路总公司相关负责人表示,到2018年底,全国铁路营业里程达到13.1万公里,其中高铁营业里程2.9万公里,超过世界高铁总里程的三分之二,下图是2014年到2018年铁路和高铁运营里程(单位:万公里)的折线图,以下结论不正确的是( )

A.每相邻两年相比较,2014年到2015年铁路运营里程增加最显著
B.从2014年到2018年这5年,高铁运营里程与年价正相关
C.2018年高铁运营里程比2014年高铁运营里程增长80%以上
D.从2014年到2018年这5年,高铁运营里程数依次成等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]()
![]() 在椭圆
在椭圆![]()
![]() 上,且椭圆的离心率为
上,且椭圆的离心率为![]() .
.
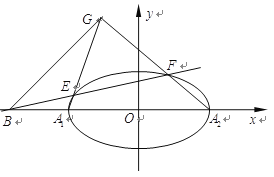
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)记椭圆的左、右顶点分别为![]() ,过点
,过点![]() 或
或![]() 作一条直线交椭圆
作一条直线交椭圆![]() 于
于![]() 、
、![]() (不与
(不与![]() 重合)两点,直线
重合)两点,直线![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .
.
①对于给定的![]() ,求
,求![]() 的值;
的值;
②是否存在一个定值![]() 使得
使得![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com