
分析 把已知的等式化切为弦,求出sin$αcosα=\frac{1}{2}$,再由sin4α+cos4α=(sin2α+cos2α)2-2(sinαcosα)2得答案.
解答 解:由tanα+cotα=2,得$\frac{sinα}{cosα}+\frac{cosα}{sinα}=2$,
即$\frac{1}{sinαcosα}=2$,∴sin$αcosα=\frac{1}{2}$,
则sin4α+cos4α=(sin2α+cos2α)2-2(sinαcosα)2=$1-2×\frac{1}{4}=\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查同角三角函数基本关系式的应用,考查灵活变形能力,是基础题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:填空题
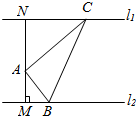 如图,A是两条平行直线之间的一定点,且点A到两平行直线的距离分别为AM=1,AN=$\sqrt{2}$,设△ABC,AC⊥AB,且顶点B、C分别在两平行直线上运动,则
如图,A是两条平行直线之间的一定点,且点A到两平行直线的距离分别为AM=1,AN=$\sqrt{2}$,设△ABC,AC⊥AB,且顶点B、C分别在两平行直线上运动,则查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 焦点在X轴上的椭圆 | B. | 焦点在Y轴上的椭圆 | ||
| C. | 焦点在X轴上的双曲线 | D. | 焦点在Y轴上的双曲线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com