
【题目】某工厂拟建一座平面图(如右图所示)为矩形且面积为200平方米的三级污水处理池,由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖).

(1)写出总造价y(元)与污水处理池长x(米)的函数关系式,并指出其定义域;
(2)求污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求最低总造价.
科目:高中数学 来源: 题型:
【题目】中央政府为了对应因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65的人群中随机调查50人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
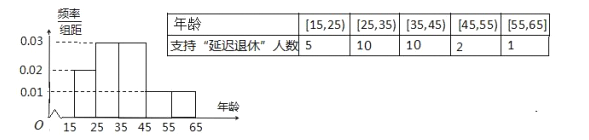
(1)由以上统计数据填下面2×2列联表,并问是否有90%的把握认为以45岁为分界点对“延迟退休年龄政策”的支持度有差异:
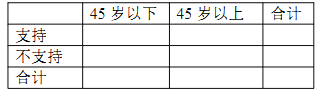
(2)若从年龄在![]() ,
,![]() 的被调查人中各随机选取两人进行调查,记选中的4人中支持“延迟退休”人数为
的被调查人中各随机选取两人进行调查,记选中的4人中支持“延迟退休”人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
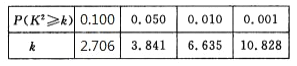
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
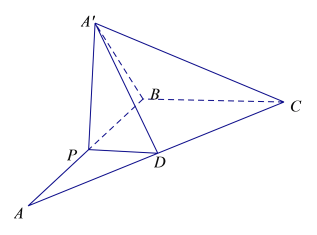
【题目】如图,在![]() 中,
中,![]()
![]() ,P为AB上一动点,
,P为AB上一动点,![]() 交于AC于点D,现将
交于AC于点D,现将![]() 沿PD翻折至
沿PD翻折至![]() ,使平面
,使平面![]() 平面PBCD.
平面PBCD.
(1)若![]() ,求棱锥
,求棱锥![]() 的体积;
的体积;
(2)若点P为AB的中点,求证:平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
, ![]() ,过
,过![]() 与坐标轴不垂直的直线
与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() ,
, ![]() 的中点为
的中点为![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求实数
?若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com