
【题目】如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M. 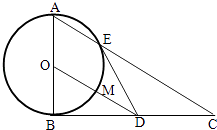
(1)求证:O、B、D、E四点共圆;
(2)求证:2DE2=DMAC+DMAB.
【答案】
(1)解:连接BE、OE,则
∵AB为圆0的直径,∴∠AEB=90°,得BE⊥EC,
又∵D是BC的中点,
∴ED是Rt△BEC的中线,可得DE=BD.
又∵OE=OB,OD=OD,∴△ODE≌△ODB.
可得∠OED=∠OBD=90°,
因此,O、B、D、E四点共圆

(2)解:延长DO交圆O于点H,
∵DE⊥OE,OE是半径,∴DE为圆O的切线.
可得DE2=DMDH=DM(DO+OH)=DMDO+DMOH.
∵OH= ![]() ,OD为△ABC的中位线,得DO=
,OD为△ABC的中位线,得DO= ![]() ,
,
∴ ![]() ,化简得2DE2=DMAC+DMAB
,化简得2DE2=DMAC+DMAB
【解析】(1)连接BE、OE,由直径所对的圆周角为直角,得到BE⊥EC,从而得出DE=BD= ![]() ,由此证出△ODE≌△ODB,得∠OED=∠OBD=90°,利用圆内接四边形形的判定定理得到O、B、D、E四点共圆;(2)延长DO交圆O于点H,由(1)的结论证出DE为圆O的切线,从而得出DE2=DMDH,再将DH分解为DO+OH,并利用
,由此证出△ODE≌△ODB,得∠OED=∠OBD=90°,利用圆内接四边形形的判定定理得到O、B、D、E四点共圆;(2)延长DO交圆O于点H,由(1)的结论证出DE为圆O的切线,从而得出DE2=DMDH,再将DH分解为DO+OH,并利用
OH= ![]() 和DO=
和DO= ![]() ,化简即可得到等式2DE2=DMAC+DMAB成立.
,化简即可得到等式2DE2=DMAC+DMAB成立.


科目:高中数学 来源: 题型:
【题目】给出下列命题:
①直线l的方向向量为![]() =(1,﹣1,2),直线m的方向向量
=(1,﹣1,2),直线m的方向向量![]() =(2,1,﹣
=(2,1,﹣![]() ),则l与m垂直;
),则l与m垂直;
②直线l的方向向量![]() =(0,1,﹣1),平面α的法向量
=(0,1,﹣1),平面α的法向量![]() =(1,﹣1,﹣1),则l⊥α;
=(1,﹣1,﹣1),则l⊥α;
③平面α、β的法向量分别为![]() =(0,1,3),
=(0,1,3),![]() =(1,0,2),则α∥β;
=(1,0,2),则α∥β;
④平面α经过三点A(1,0,﹣1),B(0,1,0),C(﹣1,2,0),向量![]() =(1,u,t)是平面α的法向量,则u+t=1.
=(1,u,t)是平面α的法向量,则u+t=1.
其中真命题的是______.(把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x+1)2+y2=20,点B(l,0).点A是圆C上的动点,线段AB的垂直平分线与线段AC交于点P.
(1)求动点P的轨迹C1的方程;
(2)设 ![]() ,N为抛物线C2:y=x2上的一动点,过点N作抛物线C2的切线交曲线Cl于P,Q两点,求△MPQ面积的最大值.
,N为抛物线C2:y=x2上的一动点,过点N作抛物线C2的切线交曲线Cl于P,Q两点,求△MPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
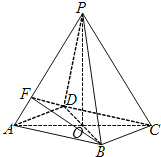
【题目】如图所示,在四棱锥![]() 中,底面四边形ABCD是菱形,
中,底面四边形ABCD是菱形, ![]() 是边长为2的等边三角形,
是边长为2的等边三角形, ![]() ,
, ![]() .
.
![]() Ⅰ
Ⅰ![]() 求证:
求证: ![]() 底面ABCD;
底面ABCD;
![]() Ⅱ
Ⅱ![]() 求直线CP与平面BDF所成角的大小;
求直线CP与平面BDF所成角的大小;
![]() Ⅲ
Ⅲ![]() 在线段PB上是否存在一点M,使得
在线段PB上是否存在一点M,使得![]() 平面BDF?如果存在,求
平面BDF?如果存在,求![]() 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com