
【题目】已知函数![]() .
.
(1)求不等式![]() 的解集;
的解集;
(2)若直线![]() 与
与![]() 的图象所围成的多边形面积为
的图象所围成的多边形面积为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1) ![]() (2)4
(2)4
【解析】
(Ⅰ)去掉绝对值号,得到分段函数,分类讨论即可求解不等式的解集,得到答案;
(Ⅱ)画出函数![]() 的图象,得出直线
的图象,得出直线![]() 与函数
与函数![]() 围成的图形,利用梯形的面积公式,即可求解.
围成的图形,利用梯形的面积公式,即可求解.
(Ⅰ)由题意,可得函数f(x)=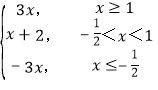 ,
,
由f(x)≥3可知:
(i)当x≥1时,3x≥3,即x≥1;
(ii)当-![]() <x<1时,x+2>3,即x≥1,与-
<x<1时,x+2>3,即x≥1,与-![]() <x<1矛盾,舍去;
<x<1矛盾,舍去;
(iii)当x≤-![]() 时,-3x≥3,即x≤-1;
时,-3x≥3,即x≤-1;
综上可知解集为{x|x≤-1或x≥1}.
(Ⅱ)画出函数y=f(x)的图象,如图所示,其中A(-![]() ,
,![]() ),B(1,3),
),B(1,3),
由kAB=1,知y=x+a图象与直线AB平行,若要围成多边形,则a>2.
易得y=x+a与y=f(x)图象交于两点C(![]() ,
,![]() ),D(-
),D(-![]() ,
,![]() ),则|CD|=
),则|CD|=![]() |
|![]() +
+![]() |=
|=![]() a.
a.
平行线AB与Cd间的距离d=![]() =
=![]() ,且|AB|=
,且|AB|=![]() ,
,
∴梯形ABCD的面积S=![]()
![]() =
=![]() (a-2)=
(a-2)=![]() ,(a>2).
,(a>2).
即(a+2-(a-2)=12,∴a=4,
故所求实数a的值为4.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是双曲线
是双曲线![]() :
:![]() 的右焦点,
的右焦点,![]() 是
是![]() 左支上的点,已知
左支上的点,已知![]() ,则
,则![]() 周长的最小值是_______.
周长的最小值是_______.
【答案】![]()
【解析】
设左焦点为![]() ,利用双曲线的定义,
,利用双曲线的定义,![]() 得到当
得到当![]() 三点共线时,三角形
三点共线时,三角形![]() 的周长取得最小值,并求得最小的周长.
的周长取得最小值,并求得最小的周长.
设左焦点为![]() ,根据双曲线的定义可知
,根据双曲线的定义可知![]() ,所以三角形
,所以三角形![]() 的周长为
的周长为![]() ,当
,当![]() 三点共线时,
三点共线时,![]() 取得最小值,三角形
取得最小值,三角形![]() 的周长取得最小值.
的周长取得最小值. ![]() ,故三角形周长的最小值为
,故三角形周长的最小值为![]() .
.
【点睛】
本小题主要考查双曲线的定义,考查三角形周长最小值的求法,属于中档题.
【题型】填空题
【结束】
16
【题目】已知![]() 分别是双曲线
分别是双曲线![]() 的左、右焦点,过点
的左、右焦点,过点![]() 作垂直与
作垂直与![]() 轴的直线交双曲线于
轴的直线交双曲线于![]() ,
,![]() 两点,若
两点,若![]() 为锐角三角形,则双曲线的离心率的取值范围是_______.
为锐角三角形,则双曲线的离心率的取值范围是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() 个数
个数![]() 的“倒均值”
的“倒均值”![]() .
.
(1)若数列![]() 的前
的前![]() 项,
项,![]() 的“倒均值”
的“倒均值”![]() . 求
. 求![]() 的通项公式
的通项公式
(2)在(1)的条件下,令![]() ,试研究数列
,试研究数列![]() 的单调性,并给出证明.
的单调性,并给出证明.
(3)在(2)的条件下,设函数![]() ,对于数列
,对于数列![]() ,是否存在实数
,是否存在实数![]() ,使得当
,使得当![]() 时,
时,![]() 对任意
对任意![]() 恒成立?若存在,求出在最小的实数
恒成立?若存在,求出在最小的实数![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长为
为边长为![]() 的正方形,
的正方形,![]() ,
,![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中.
中.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在棱
在棱![]() 上,满足
上,满足![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,求
,求![]() 得取值范围.
得取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】条形图给出的是2017年全年及2018年全年全国居民人均可支配收入的平均数与中位数,饼图给出的是2018年全年全国居民人均消费及其构成,现有如下说法:
①2018年全年全国居民人均可支配收入的平均数的增长率低于2017年;
②2018年全年全国居民人均可支配收入的中位数约是平均数的![]() ;
;
③2018年全年全国居民衣(衣着)食(食品烟酒)住(居住)行(交通通信)的支出超过人均消费的![]() .
.
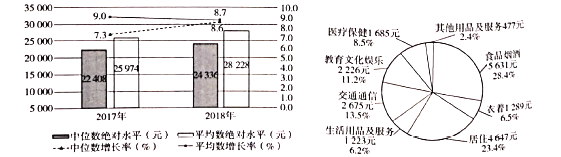
则上述说法中,正确的个数是( )
A. 3B. 2C. 1D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com